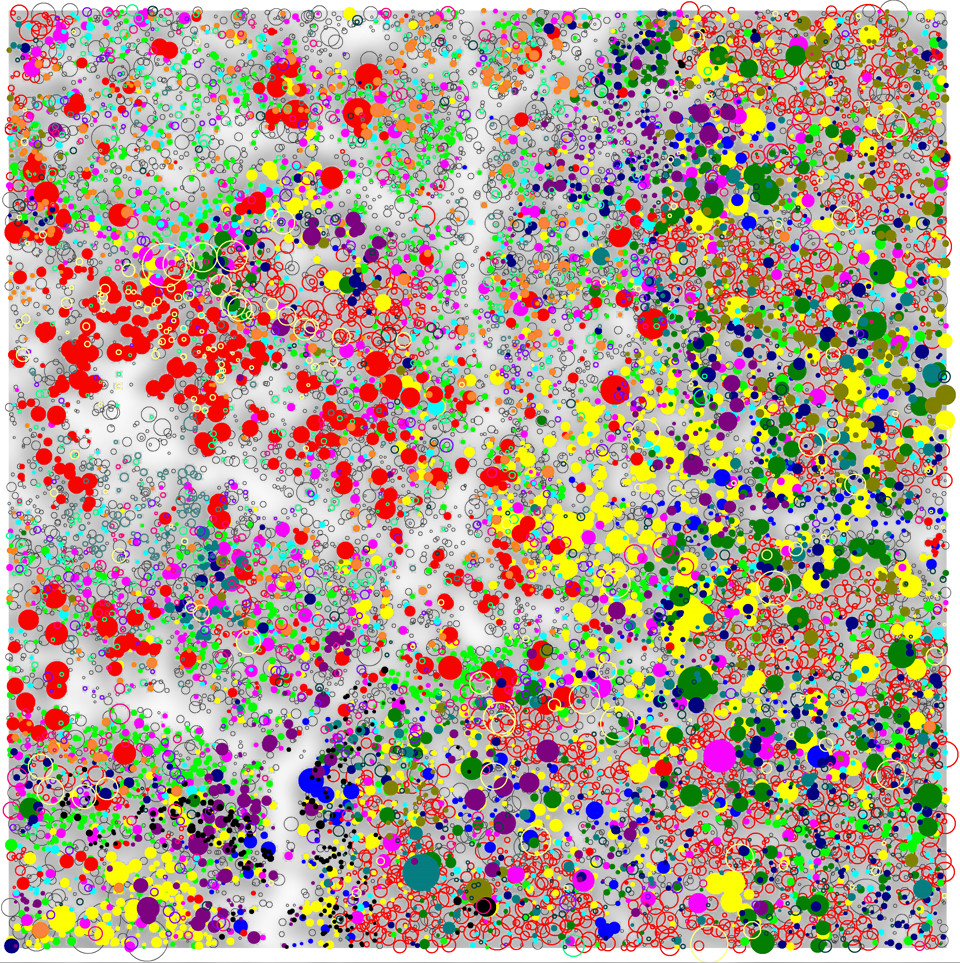
Tropical forests are not only extraordinary rich in tree species, they also hide spatial patterns of amazing harmony, almost like a piece of modern art. The image represents the spatial position and size of larger trees in a 500m x 500m plot of tropical forest in Sri Lanka. Different colors indicate different species.
Should the information hidden in these spatial patterns convey information about the underlying ecological mechanisms or even conceal the key to coexistence? The ERC advanced grant project SpatioCoexistence will find out. We will take advantage of spatial scaling to incorporate this detailed spatial information into mathematical coexistence theory.
Towards a Spatial Theory for Species-Rich Communities
ERC advanced grant 2024-2029
Summary
Ecologists have tried for long to explain coexistence of many competing species in communities such as tropical forests, but this key question of ecological theory remains largely unresolved. We argue that this failure originates as a scaling problem. Although plants compete mostly with their closest neighbors, the phenomenological models of most approaches addressing this question do not consider spatial mechanisms of how the dynamics and patterns at the “macroscopic” community scale emerge from the collective behavior and interactions of individuals at the “microscopic” neighborhood scale. We therefore propose to change the way the problem is tackled by incorporating this essential information into macroscopic mathematical models.
The overarching ecological objective of SpatioCoexistence is to develop a spatially-explicit theory for forest communities of intermediate to high tree species richness, as found for example in temperate, subtropical and tropical forests, to derive theoretical expectations about how multiple ecological pattern and processes interact in determining the dynamics and coexistence of species in empirical settings. We integrate state-of-the-art mathematical and simulation approaches with methods from physics and spatial analysis of the large spatial data sets, such as ForestGEO inventory data of 20-50 ha forest plots, each comprising the species identity, size and location of >100,000 trees. The link to the microscopic scale of individual plants allows us to integrate ecological detail in unprecedented ways, while keeping the theory tractable.
Spatial scaling allows us to transfer the critical spatial information from the microscopic scale into commonly used macroscopic multispecies models. This requires synthesizes of several well established, but so far isolated approaches, including methods of spatial point process theory and physics to derive novel individual-based neighborhood competition indices based on stochastic geometry and sphere packing. The parameters of macroscopic multispecies models will be replaced by transfer functions that result from scale-transition theory by non-linear averaging of individual plant performance and depend on species demography, traits and indices of spatial patterns. The project will provide theoretical expectations and mechanistic understanding of how multiple (spatial) pattern and processes shape species richness, and reveal if simple laws govern the assembly and dynamics of complex species-rich communities. This project open the door to new research lines of spatial ecology to better understand and conserve biodiversity.
Spatial data Analysis
Spatial data analysis ties our theory to observed data. We quantify the richness of multispecies spatial patterns observed in forest inventories (e.g., ForestGEO), high-resolution lidar data and process-based forest simulators using spatial point process theory. The spatial analysis serves three main tasks, it quantifies suitable competition indices that form the heart of the transfer functions, it reveals general relationships and latitudinal patterns of spatial patterns to be included into the theory, and the detected spatial patterns serve as benchmark for testing and validating our theory.
General principles of stochastic geometry will guide development of neighborhood competition indices from mechanistic assumptions on how plant performance (e.g., survival) is influenced by interactions with neighbors, such as crowding competition through competition for space, light or nutrients, or natural enemies. Suitable crowding indices will be selected by statistical models using spatially explicit data on tree growth and survival, and data on species traits and environmental variables. The challenge here is to develop competition indices that accommodate sufficient biological detail (e.g., on the distance, size, and niche differences of neighbors) to allow e.g., inclusion of basic trade-offs (e.g., growth-survival and stature-recruitment), but keep the resulting theory tractable.
Individual-based biodiversity simulation models
Individual-based biodiversity simulation models (IBBs) allow ecologists to understand natural complexity and how it emerges from the variability and adaptability of individual organisms. Enormous increases in computing power allow now simulation of large numbers of individuals in virtual communities. IBBs are especially needed in SpatioCoexistence for implementing and testing the mathematical theory. They fulfil a key-mediating role between spatial data analysis and mathematical theory for exploring how spatial patterns emerge from microscopic mechanisms such as animal seed dispersal or canopy gaps. Specifically, IBBs will test the transfer functions that transport the critical micro- and mesoscopic information into the macroscopic theory. The IBBs will include the basic processes of recruitment, competition, size growth, and mortality, depending on a minimal set of spatial mechanisms such as seed dispersal, competition indices based on neighborhood spatial patterns and individual-level interaction coefficients (derived from species traits), habitat filtering, and the effect of environmental variance.
Mathematical Theory and Models
Our novel methodological contributions to ecological theory are linking macroscopic models via transfer functions to microscopic behavior and emerging mesoscopic patterns, and taking advantage of simplicity emerging from complex interactions in species-rich communities. The underlying rationale of linking microscopic and macroscopic scales is given by the powerful adiabatic technique used in physics (separation of time scales): variables describing spatial patterns converge much quicker than macroscopic state variables. We need therefore not to solve the dynamics of the pattern variables analytically, but introduce them as parameters into the model, while their values can be inferred from spatial analysis of ForestGEO data. Technically, this can be accomplished by applying scale-transition theory.
Given that the possibility of manipulative experiments is limited, we further develop and test our theory with in silicio biodiversity experiments based on detailed process-based forest simulators that integrate recent advances in plant physiology and demography to commonly collected species-specific functional traits. These models are parameterized by measurable species traits, which provides us the unique possibility to conduct a systematic mapping of this detailed model to our analytical theory and to reveal direct links between species traits, indices of spatial patterns and community dynamics.
References
Wiegand T., et al. 2021. Consequences of spatial patterns for coexistence in species rich plant communities. Nature Ecology and Evolution 5: 965–973
Wiegand T, Huth A., and X. Wang. 2021. Behind the paper: Space can change what we think we know about coexistence.
Wiegand T., et al. 2024. Latitudinal scaling of aggregation with abundance and its consequences for coexistence in species rich forests. bioRxiv preprint