WP 2: Pathways through pressure-driven percolation
News (December 2022)
In CAU, we continued performing the fluid percolation experiments to further investigate the influences of structural anisotropy and in-situ stress field on behavior of hydraulically driven fractures in Opalinus clay. The tests were performed using the true triaxial device. To trace the fracture propagation path inside the cubic Opalinus clay sample a fluorescent oil was employed as the fracturing fluid. The experiment starts as the sample reaches the mechanical equilibrium with the applied stress field and terminates with observation of the breakdown pressure. After finishing the experiment, the retrieved sample was cut into different cross sections. Fig.1 illustrates examples of the fracture pattern marked by the fluorescent oil under the UV light. Based on the applied stress field and the bedding direction, pressure-induced fractures can either follow a straight path or form a complex fracture network before reaching the sample surface. Further details regarding the test setup and obtained experimental results can be found in the GeomInt2 book
 Figure 1. Fracture path on the sample surface, cross-section cuts and inner fracture propagation path for samples with scaled borehole (a) perpendicular to bedding direction, (b) parallel to bedding direction, and (c) oblique to the bedding direction.
Figure 1. Fracture path on the sample surface, cross-section cuts and inner fracture propagation path for samples with scaled borehole (a) perpendicular to bedding direction, (b) parallel to bedding direction, and (c) oblique to the bedding direction.
[IfG] After implementing a continuum-mechanical version of its discontinuum-mechanical percolation model for fluid flow in salt rocks using a full-tensor anisotropy formulation depending on fluid pressures and acting rock stresses using a meshfree finite-volume Godunov-scheme, a numerical recalculation of a large-scale in situ test was to be performed in order to demonstrate the capabilities and accuracy of the new approach. In this in situ test, a 60m long borehole with a diameter of 1,35 m was drilled between to mining levels of a salt mine and additionally monitored by a seismic array. The borehole was cemented in the lower part, leaving a 40m high cylindrical cavity which was then pressurized with gas. In accordance with the expected stress field, the salt borehole was gas-tight until the gas pressures reached a level above the minimum principle stress at the lower end of the borehole. The thereby created percolation front started in the bottom part of the borehole (at the cement plug) and progressed in a nearly horizontal plane above the underground mine drifts, which was to be replicated by the newly developed method. The hydro-mechanically coupled calculations of the percolation reaction in response to the stepwise increase of borehole pressure successfully confirm the in situ observations (Fig. 1).
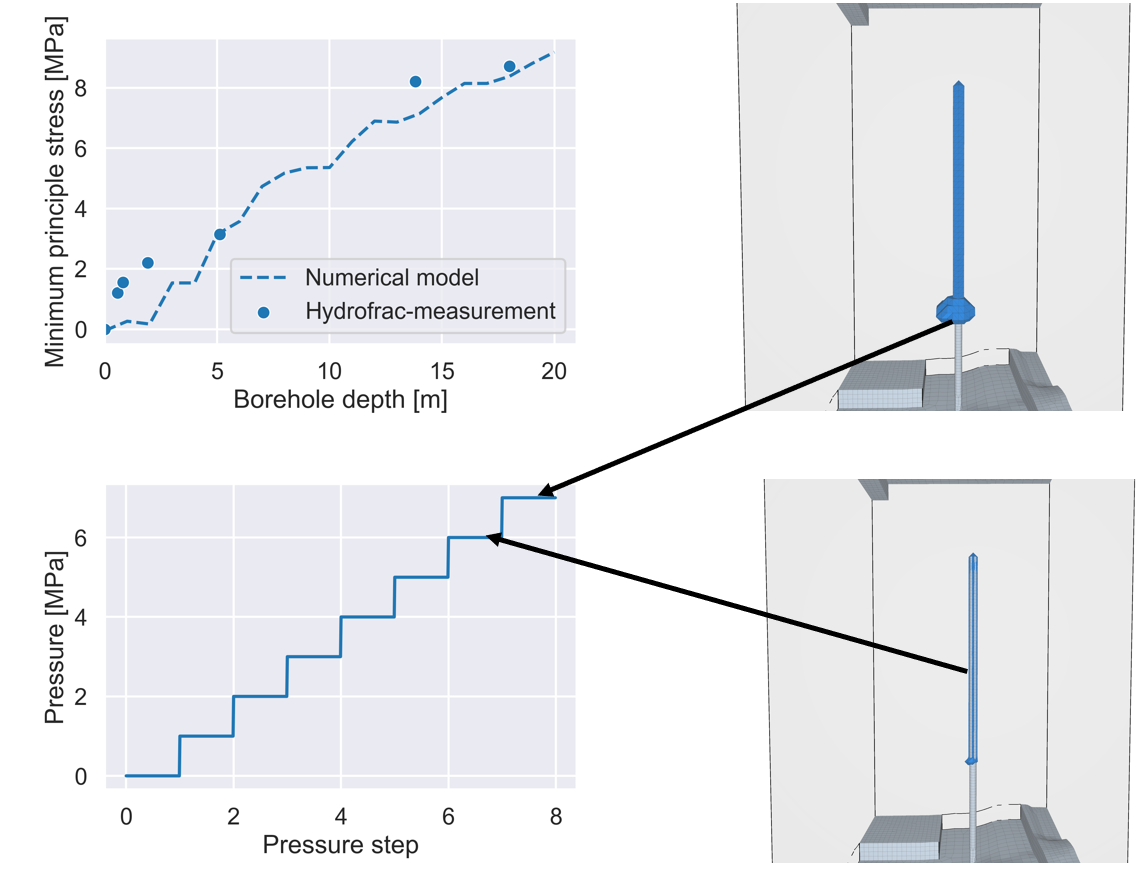 Fig. 1: Recalculation of a large scale in-situ borehale pressurization test. Calibration of stress field against hydrofrac-measurements (top left) and modeled onset of percolation upon exceeding a threshold pressure in a nearly horizontally aligned plane at the bottom of the pressurized cavity.
Fig. 1: Recalculation of a large scale in-situ borehale pressurization test. Calibration of stress field against hydrofrac-measurements (top left) and modeled onset of percolation upon exceeding a threshold pressure in a nearly horizontally aligned plane at the bottom of the pressurized cavity.
Using the novel MHD-approach, the modeled borehole is tight against the attacking gas pressure until the minimum principle stress is exceeded, which happens first in the lowest part of the borehole. The direction of the percolation plane is oriented perpendicular to the smallest compressive stress and therefore nearly horizontally aligned. The percolation front in the in situ test eventually hit a almost perfectly horizontal weakness plane and is therefore slightly more localized, which is not included in this modeling. However, the new method has shown to well suited to model the pressure- and stress-tensor-dependent salt percolation process both in laboratory and in situ scale remarkably well.
 Fig. 2: Failure Pattern of Opalinus clay where layering is (a) parallel, (b) 45 degrees inclined and (c) perpendicular to loading path
Fig. 2: Failure Pattern of Opalinus clay where layering is (a) parallel, (b) 45 degrees inclined and (c) perpendicular to loading path
[CAU] In the geomechanical laboratory of CAU, the experimental studies are being continued in order to characterize the anisotropic behavior of Opalinus clay.
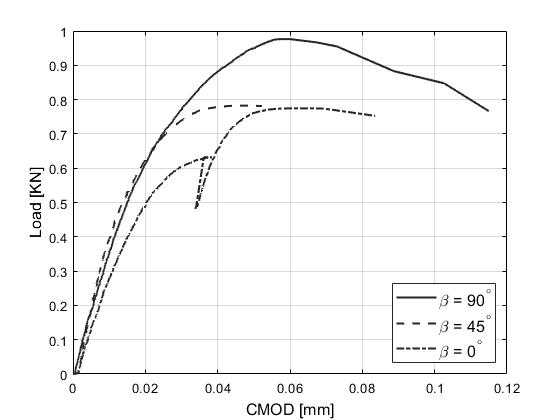 Fig. 3: Comparison of Load-CMOD curves for β = 0/45/90 deg (β: degree between layering and load path)
In Fig. 2, failure pattern of three Opalinus clay SCB (Semi-Circular Bending) samples with three different layering direction of 0, 45 and 90 is presented. The samples belong to A26 borehole core. The failure patterns indicate the dependence of fracture path trajectory to the layering directions. Furthermore, with use of a clip gauge extensometer, the unique Load-CMOD curves are obtained for each case and shown if Fig. 3. Parallelly, the three-point bending tests in the customized desiccator cell are being carried out in order to obtain water content dependent mechanical properties of Opalinus clay in various isotropy planes.
Fig. 3: Comparison of Load-CMOD curves for β = 0/45/90 deg (β: degree between layering and load path)
In Fig. 2, failure pattern of three Opalinus clay SCB (Semi-Circular Bending) samples with three different layering direction of 0, 45 and 90 is presented. The samples belong to A26 borehole core. The failure patterns indicate the dependence of fracture path trajectory to the layering directions. Furthermore, with use of a clip gauge extensometer, the unique Load-CMOD curves are obtained for each case and shown if Fig. 3. Parallelly, the three-point bending tests in the customized desiccator cell are being carried out in order to obtain water content dependent mechanical properties of Opalinus clay in various isotropy planes.
[CAU] The experimental configuration of Figure 1a, including the loading frame of three-point bending test, a microscopic camera and an extensometer, was set up in geotechnical laboratory of Kiel University to investigate the correctness of displacement measurements using the microscopic camera. The clip gauge extensometer was used to measure the exact crack mouth opening displacement (CMOD) of Opalinus Clay sample during the experiment (Figure 1b).
 Fig. 1(a): The experimental setup
Fig. 1(a): The experimental setup
 Fig. 1(b): Mounted clip gauge extensometer on the specimen
Fig. 1(b): Mounted clip gauge extensometer on the specimen
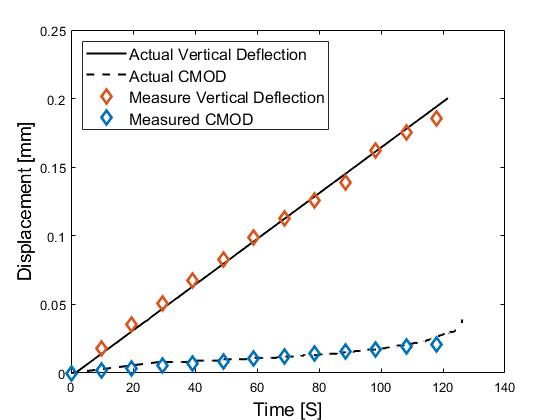 Fig. 2: Comparison between actual and measured displacements using image processing
At the same time, the digital microscopic camera was used to track the displacement across the sample at 35X magnification scale. It can be seen from the data reported in Figure 2 that the actual measured displacements and the approximated displacements, by aid of image processing and computer vision, are in good agreement. This setup will further be used in the customized desiccator cell where physical measurements of CMOD are not available
Fig. 2: Comparison between actual and measured displacements using image processing
At the same time, the digital microscopic camera was used to track the displacement across the sample at 35X magnification scale. It can be seen from the data reported in Figure 2 that the actual measured displacements and the approximated displacements, by aid of image processing and computer vision, are in good agreement. This setup will further be used in the customized desiccator cell where physical measurements of CMOD are not available
Furthermore, in order to enhance the fluid flow module in FDEM framework, the formulation of unsaturated flow in porous medium, solving Richard’s equation, has been implemented. The implemented modules were verified by solving and comparing various infiltration and desaturation benchmark problems to both available data in literature and commercial finite element packages (Figure 3). Given FDEM’s capability in simulation of complex fracture networks and fracture branching and coalescence, solving Richards’ equation would enable us to have a better understanding of desiccation cracking around open galleries and niches where excavation damaged zones are present.
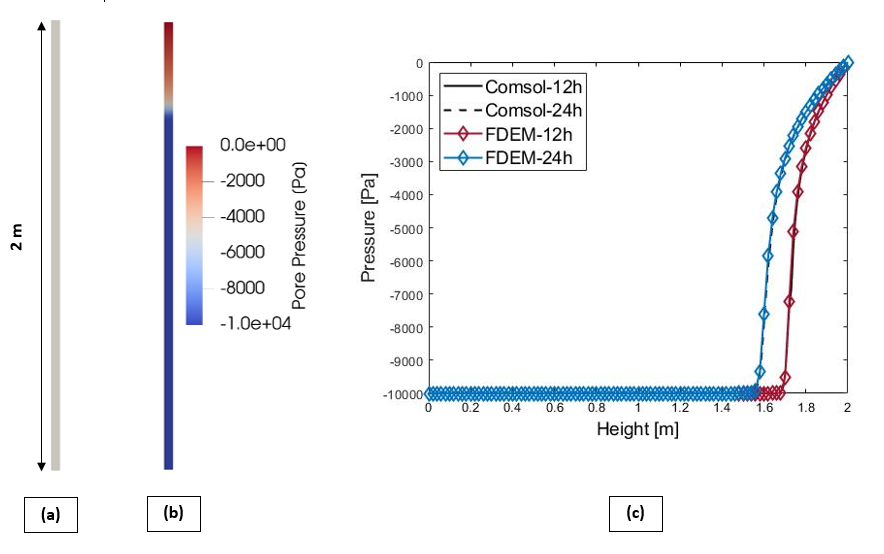 (a) Benchmark problem of an unsaturated sand column subjected to infiltration at top(b) pressure profile after 1-day (c) Comparison of FDEM results with COMSOL Multiphysics
(a) Benchmark problem of an unsaturated sand column subjected to infiltration at top(b) pressure profile after 1-day (c) Comparison of FDEM results with COMSOL Multiphysics
[IfG] In the previous steps the IfG implemented a continuum-mechanical version of its discontinuum-mechanical percolation model for fluid flow in salt rocks using a full-tensor anisotropy formulation depending on fluid pressures and acting rock stresses using a meshfree finite-volume Godunov-scheme with a higher-order gradient estimator based on an approach in magneto-hydrodynamics In addition to numerous validation examples and comparison to analytical solutions, the results of lab-scale hydro-mechanically coupled extension tests were successfully replicated using the new approach (Fig. 3).
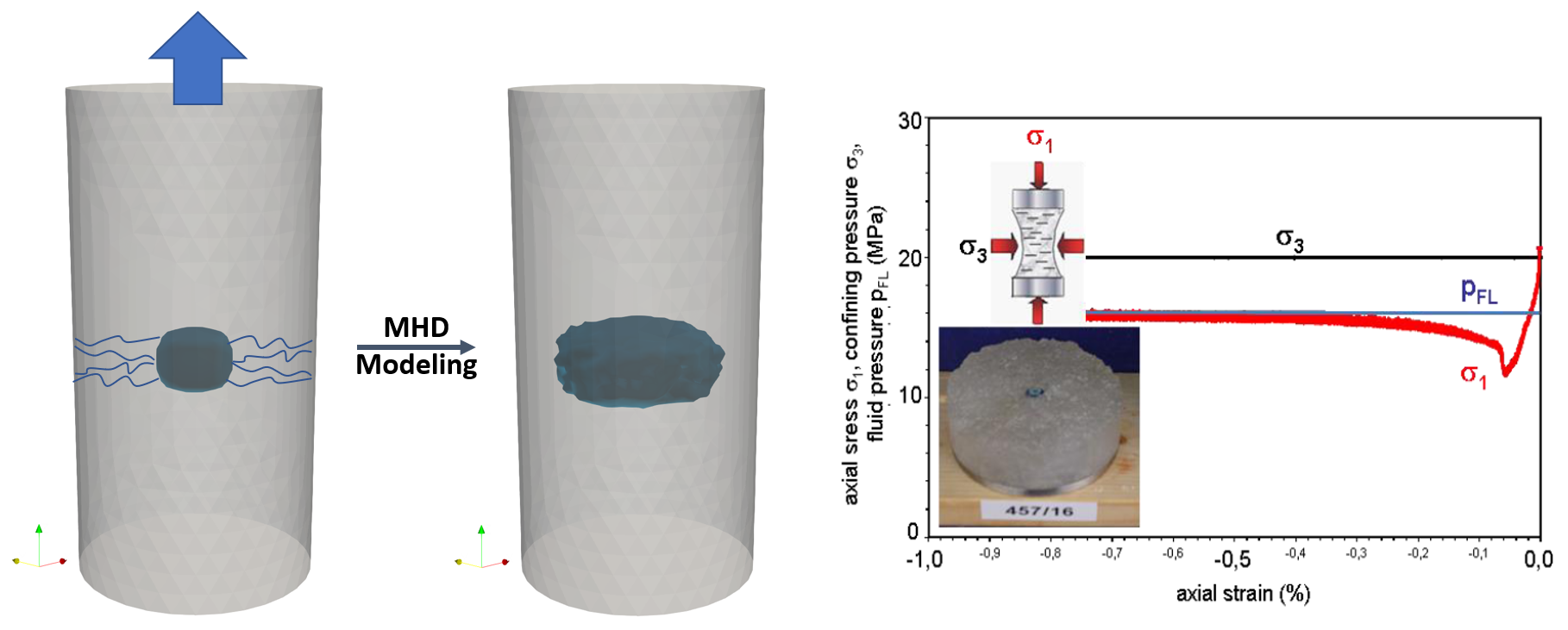 Fig. 3: MHD-Modeling of pressure-driven percolation in a triaxial extension sample.
Fig. 3: MHD-Modeling of pressure-driven percolation in a triaxial extension sample.
In the final stage, the application of the method on a large-scale real-world geomechanical application (borehole pressurization test) is currently being modeled (Fig. 4). In this test, a 60m long borehole with a diameter of 1,35 m was drilled between to mining levels of a salt mine and additionally monitored by a seismic array. The borehole was cemented in the lower part, leaving a 40m high cylindrical cavity which was then pressurized with gas. In accordance with the expected stress field, the salt borehole was gas-tight until the gas pressures reached a level above the minimum principle stress at the lower end of the borehole. The thereby created percolation front then moved in a horizontal plane above the underground mine drifts. Capturing the essential mechanisms of this in-situ tests is numerically challenging and will therefore be a valuable in-situ test-case for the developed highly anisotropic continuum-mechanical percolation approach.
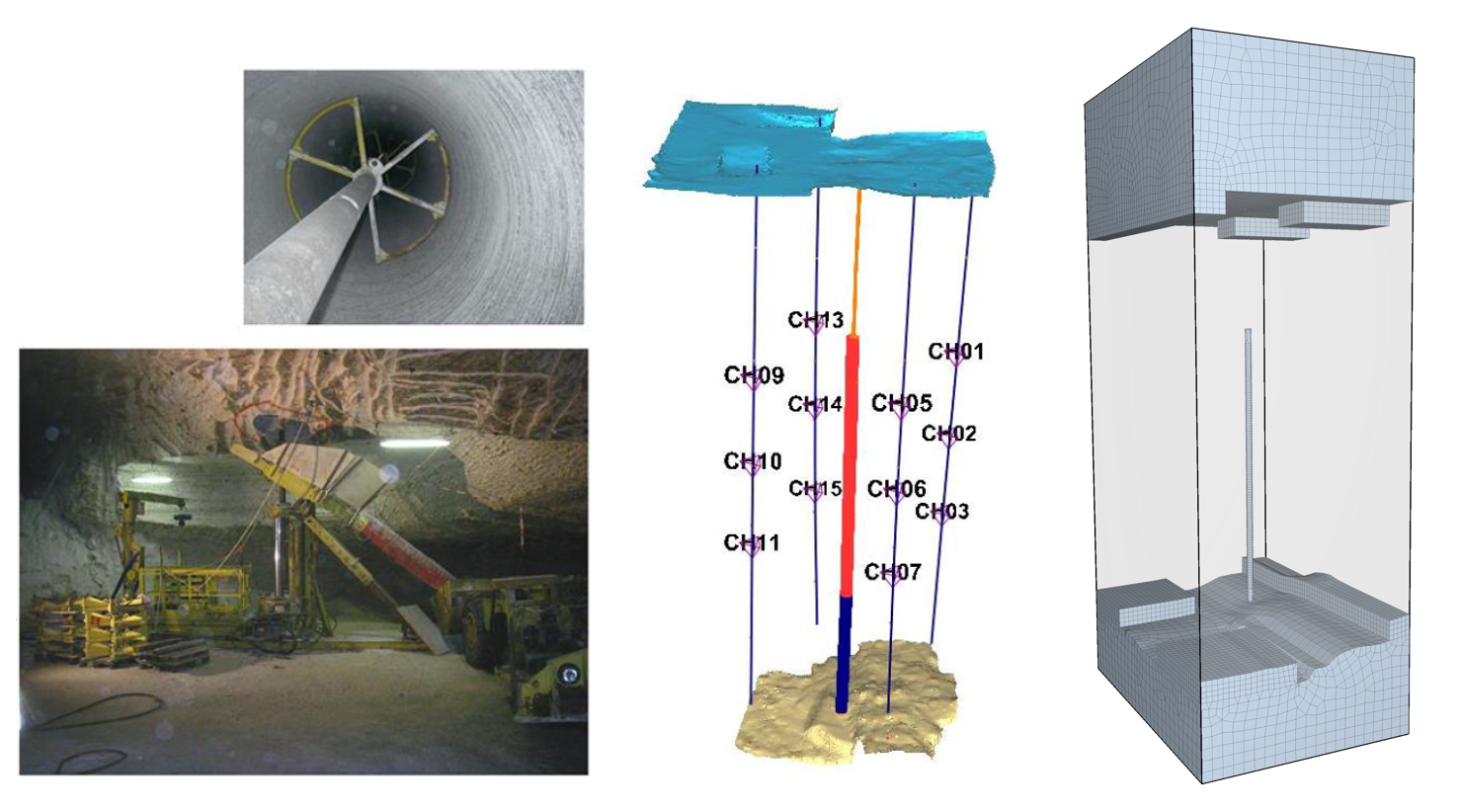 Fig. 4: Large scale in-situ borehale pressurization test (left) with acoustic emission measurement array (center) and the numerical FLAC3D model for the re-calculation of the in-situ test using the MHD approach
Fig. 4: Large scale in-situ borehale pressurization test (left) with acoustic emission measurement array (center) and the numerical FLAC3D model for the re-calculation of the in-situ test using the MHD approach
[CAU] A series of geomechanical laboratory testing, including indirect tensile strength test and unconfined compression test, has been performed on two different borehole directions of Opalinus clay core samples (see figures below). This process, integrated with back-analysis of FDEM simulations, has been adopted to characterize the transversely isotropic material constants of Opalinus Clay as well as fracture strength parameters in both parallel and perpendicular directions to plane of transverse isotropy.
 (a) Unconfined Compression Test
(a) Unconfined Compression Test
 (b) Indirect Tensile Strength Test
(b) Indirect Tensile Strength Test
For the numerical developments, a transversely isotropic stress-strain constitutive law has been adopted and the hydraulic solver implemented in FDEM framework has been improved to capture both porous media and fracture flow in a coupled manner. Furthermore, a size effect study has been performed to ensure the stability of FDEM simulations across different scales. Finally, characteristics of pressure driven fluid percolation in Opalinus clay has been studied in field-scale through different numerical test cases.
[IfG] As its contribution to the work package 2 within Geomint2, the IfG is aiming to implement a continuum-mechanical version of its discontinuum-mechanical percolation model for fluid flow in salt rocks using a full-tensor anisotropy formulation depending on fluid pressures and acting rock stresses. After an initial survey of suitable numerical approaches, we implemented a meshfree finite-volume Godunov-scheme with a higher-order gradient estimator based on an approach in magneto-hydrodynamics [1]. The scheme has been adapted to the realm of geomechanics and porous flow by the introduction of saturation and a dynamic permeability tensor based on the stress tensors and fluid pressures in the coupled mechanical FLAC3D model. The numerical capabilities and improvements over standard codes by the developed method are demonstrated using numerous validation examples and compared against analytical solutions (if available). Currently, the application of the method on a larger-scale real-world geomechanical application (borehole pressurization test) is being prepared.
[1] Philip F. Hopkins, A new class of accurate, mesh-free hydrodynamic simulation methods, Monthly Notices of the Royal Astronomical Society, Volume 450, Issue 1, 11 June 2015, Pages 53–110
[TUBAF#IfG#UFZ] The extension of fluid pathways along grain boundaries may occur in undamaged materials if the fluid pressure increases beyond the minimal principal stress and tensile strength of the grain boundaries. This circumstance causes a process called "pressure-driven percolation", which can be problematic for different subsurface structures like reservoirs, caverns or repositories and fluid leakage can occur due to higher fluid pressure inside these structures. Appropriate permeability models are the key component to describe this behaviour and to generate realistic results. A permeability model is developed, extended and implemented in OpenGeoSys to describe behaviour of polycrystalline materials during the pressure-driven percolation.
Furthermore, various models are implemented to simulate different stages of the creep process. In combination with the new permeability model, it is possible to generate more realistic results of the pressure-driven percolation process.
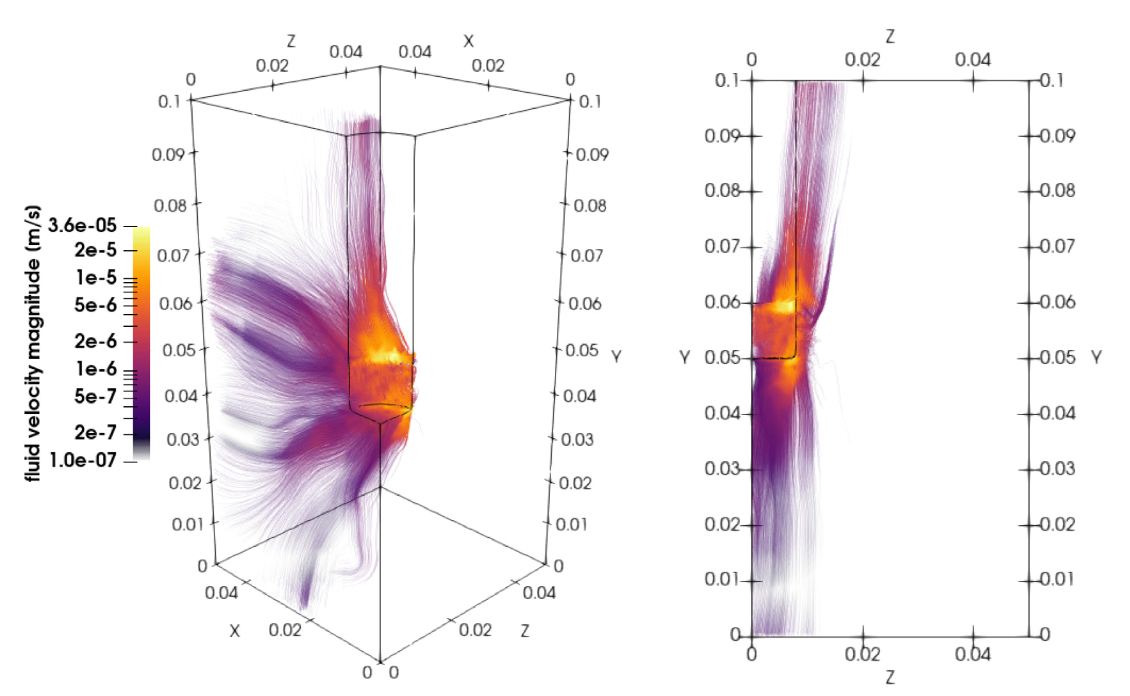 Simulated fluid motion streamlines perpendicular to the minimum principal stress in z-direction [1]
Simulated fluid motion streamlines perpendicular to the minimum principal stress in z-direction [1]
[1] F. Zill, C. Lüdeling, O. Kolditz, T. Nagel; Hydro-mechanical continuum modelling of fluid percolation through rock salt, International Journal of Rock Mechanics and Mining Sciences, Volume 147, 2021. https://doi.org/10.1016/j.ijrmms.2021.104879
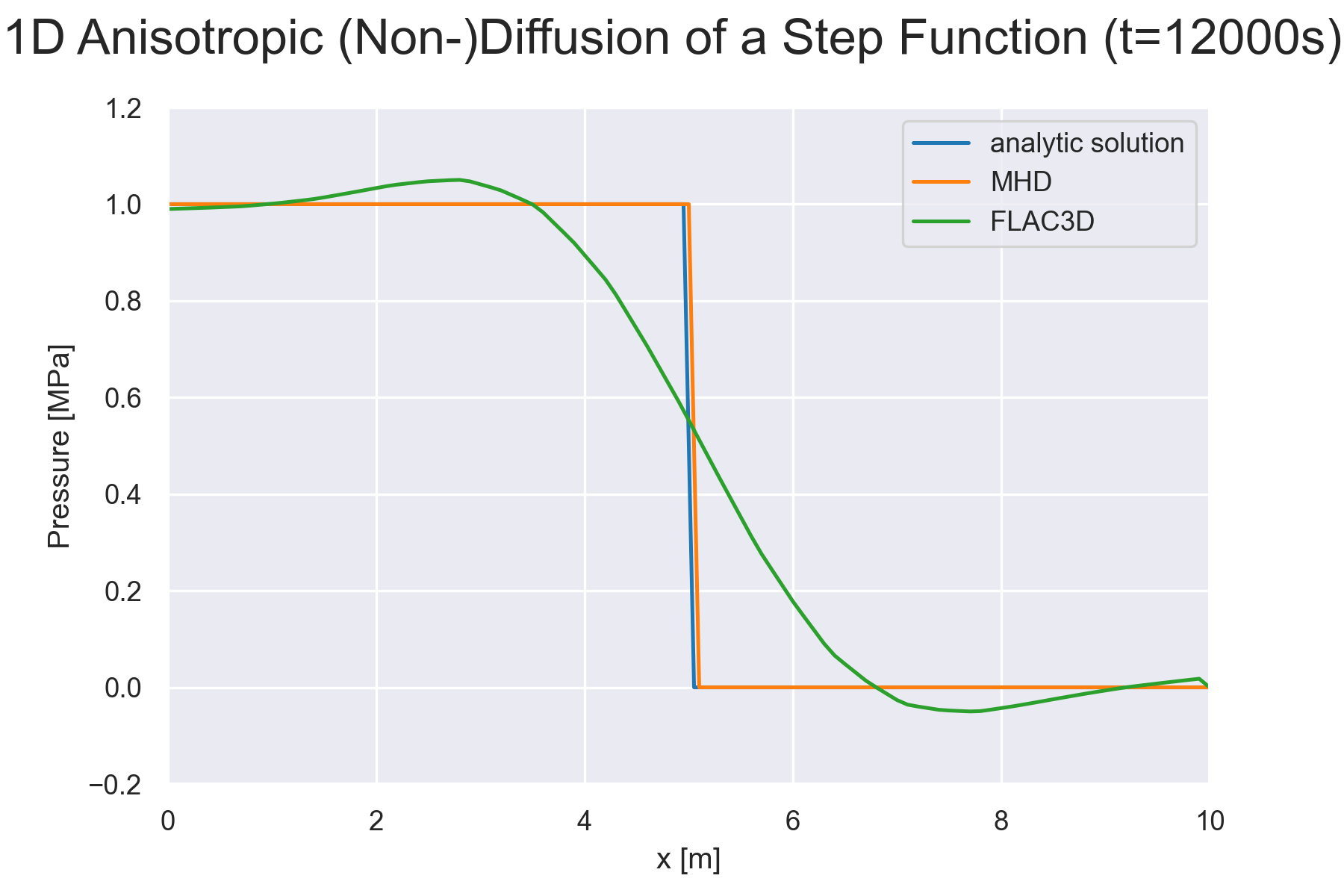
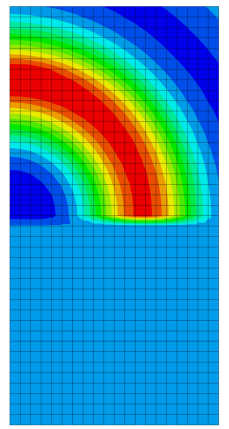 [IfG] As its contribution to the work package 2 within Geomint2, the IfG is aiming to implement a continuum-mechanical version of its discontinuum-mechanical percolation model for fluid flow in salt rocks using a full-tensor anisotropy formulation depending on fluid pressures and acting rock stresses. A newly developed published approach for mesh-free hydrodynamics [1] is currently being implemented and tested against various benchmark examples, in order to verify that the anisotropic percolation is captured accurately irrespective of the mesh structure and that the formulation keeps erroneous numerical diffusion into the wrong direction as small as possible.
[IfG] As its contribution to the work package 2 within Geomint2, the IfG is aiming to implement a continuum-mechanical version of its discontinuum-mechanical percolation model for fluid flow in salt rocks using a full-tensor anisotropy formulation depending on fluid pressures and acting rock stresses. A newly developed published approach for mesh-free hydrodynamics [1] is currently being implemented and tested against various benchmark examples, in order to verify that the anisotropic percolation is captured accurately irrespective of the mesh structure and that the formulation keeps erroneous numerical diffusion into the wrong direction as small as possible.
[1] Philip F. Hopkins, A new class of accurate, mesh-free hydrodynamic simulation methods, Monthly Notices of the Royal Astronomical Society, Volume 450, Issue 1, 11 June 2015, Pages 53–110
[CAU] Hybrid Finite/Discrete Element method (FDEM)
 [CAU] After careful inspection of the literature on simulation of the fracturing processes, the Finite Discrete Element Method (FDEM) has been selected as the base numerical framework for numerical developments of WP1 and WP2. Initially proposed by Munjiza (2004)[1], FDEM has been employed extensively in geomechanical problems to capture the characteristics of arbitrary fracture propagation and fragmentation. In fact, the FDEM considers the domain of the problem as a formation of interacting discrete bodies, which are discretized into finite elements to be able to analyze deformability, fracturing and fragmentation by means of zero-thickness elements. The leading software of the FDEM is written in the programing language of C, known as Y-code. As an initial step and a basis for further developments regarding GeomInt2, the Y-code has been completely re-written in Matlab programing language. The in-house software has been validated against examples provided by Munjiza(2004)[1]. Further developments of the FDEM would include implementation of transversely isotropic constitutive law, anisotropic fracture model and coupling the solutions with hydro-mechanical boundary conditions.
[CAU] After careful inspection of the literature on simulation of the fracturing processes, the Finite Discrete Element Method (FDEM) has been selected as the base numerical framework for numerical developments of WP1 and WP2. Initially proposed by Munjiza (2004)[1], FDEM has been employed extensively in geomechanical problems to capture the characteristics of arbitrary fracture propagation and fragmentation. In fact, the FDEM considers the domain of the problem as a formation of interacting discrete bodies, which are discretized into finite elements to be able to analyze deformability, fracturing and fragmentation by means of zero-thickness elements. The leading software of the FDEM is written in the programing language of C, known as Y-code. As an initial step and a basis for further developments regarding GeomInt2, the Y-code has been completely re-written in Matlab programing language. The in-house software has been validated against examples provided by Munjiza(2004)[1]. Further developments of the FDEM would include implementation of transversely isotropic constitutive law, anisotropic fracture model and coupling the solutions with hydro-mechanical boundary conditions.
Regarding the evaluation of fracture parameters and a benchmark for comparison of the proposed numerical method, an ISRM suggested three-point bending test, as well as a modified asymmetrical three-point bending test using semi-circular specimens have been planned[2, 3].
[1] A. A. Munjiza, The combined finite-discrete element method. John Wiley & Sons, 2004.
[2] M. D. Kuruppu, Y. Obara, M. R. Ayatollahi, K. P. Chong, and T. Funatsu, “ISRM-suggested method for determining the mode I static fracture toughness using semi-circular bend specimen,” Rock Mech. Rock Eng., vol. 47, no. 1, pp. 267–274, 2014.
[3] M. Nejati, A. Aminzadeh, M. O. Saar, and T. Driesner, “Modified semi-circular bend test to determine the fracture toughness of anisotropic rocks,” Eng. Fract. Mech., vol. 213, pp. 153–171, 2019.
As its contribution to the work package 2 within Geomint2, the IfG is aiming to implement a continuum-mechanical version of its discontinuum-mechanical percolation model for fluid flow in salt rocks using a full-tensor anisotropy formulation depending on fluid pressures and acting rock stresses. While the derivation of such a tensor formulation is fairly straightforward, the implemention of fluid diffusion in highly anisotropic fields much more demanding. If the numerical grid is not perfectly aligned with the eigenvectors of the permeability tensor - e.g. on general unstructuded grids - most standard approaches (such as the widely used two-point flow approximation) yield excessive so-called numerical diffusion into the wrong direction and also violate many desirable properties expected from numerical fluid calculations such as local conservativity or the discrete extremum principle. However, in order to model the pressure-driven percolation in a continuum-mechanical framework the employed numerical scheme must be able to keep a fluid stable within its permeabilty-defined boundaries within the large timeframes necessary for studying long-term barrier integrity. Some simple methods (such as e.g. slope-limiting) may alleviate the numerical issues at least partially, but are not sufficient long-term solutions from our experience. Therefore the IfG is currently investigating various published methods for highly anisotropic flow schemes and is evaluating their respective chances for success. Some tentative implementations have been performed to date, which showed encouraging results, but the modeling is still in an exploratory phase.
 At CAU Kiel, three samples under different stress boundary conditions undergo the fracking process using the true triaxial apparatus. According to the pre-existing mechanical stress distribution, the fracking pattern under applied hydraulic pressure is unique for each stress distribution.
At CAU Kiel, three samples under different stress boundary conditions undergo the fracking process using the true triaxial apparatus. According to the pre-existing mechanical stress distribution, the fracking pattern under applied hydraulic pressure is unique for each stress distribution.
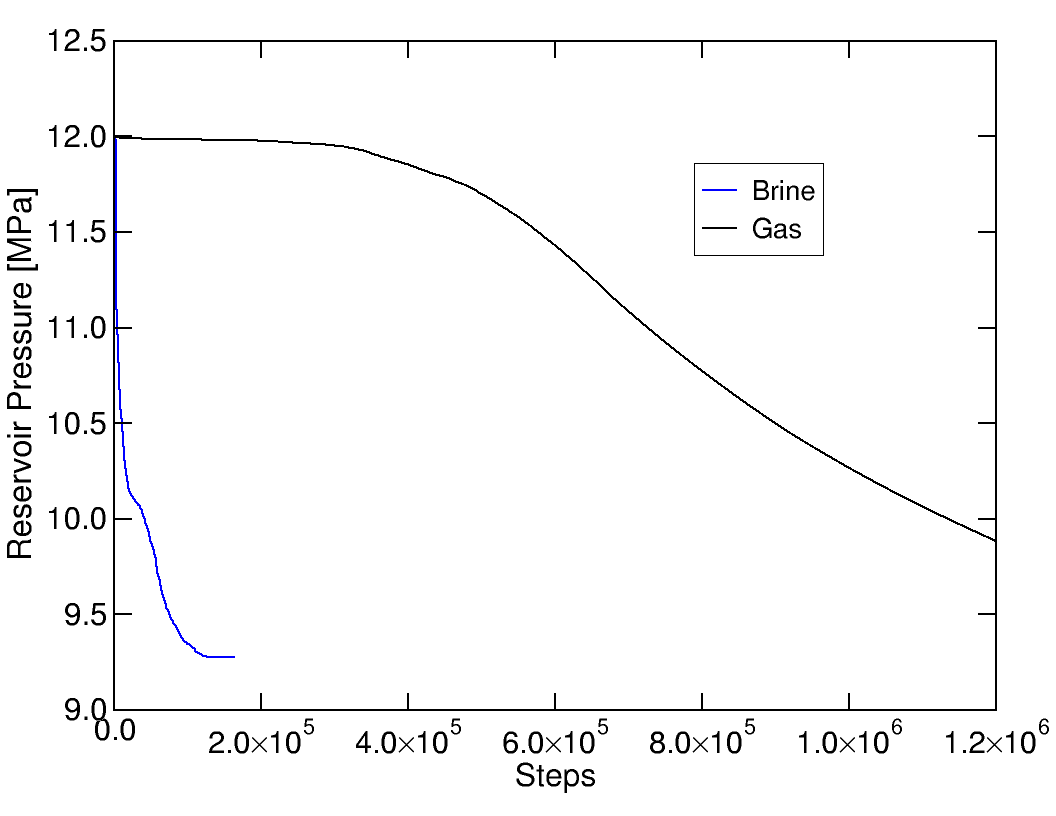
Modelling: Difference of liquids and gases in pressure driven percolation
Salt caverns are used to store natural gas and mineral gas. When they are abandoned, they are usually filled with brine and sealed. The natural convergence of the caverns leads to an increase of the pressure, which can supersede the minimal principal stress in the contour. The cracks that form provide an additional accessible volume, to which the fluid reacts with a change of pressure. As the bulk moduli of liquids and gases are very different, there corresponding reaction is different, too. We modelled this process for an experiment on lab scale, and could reproduce the expected responses.
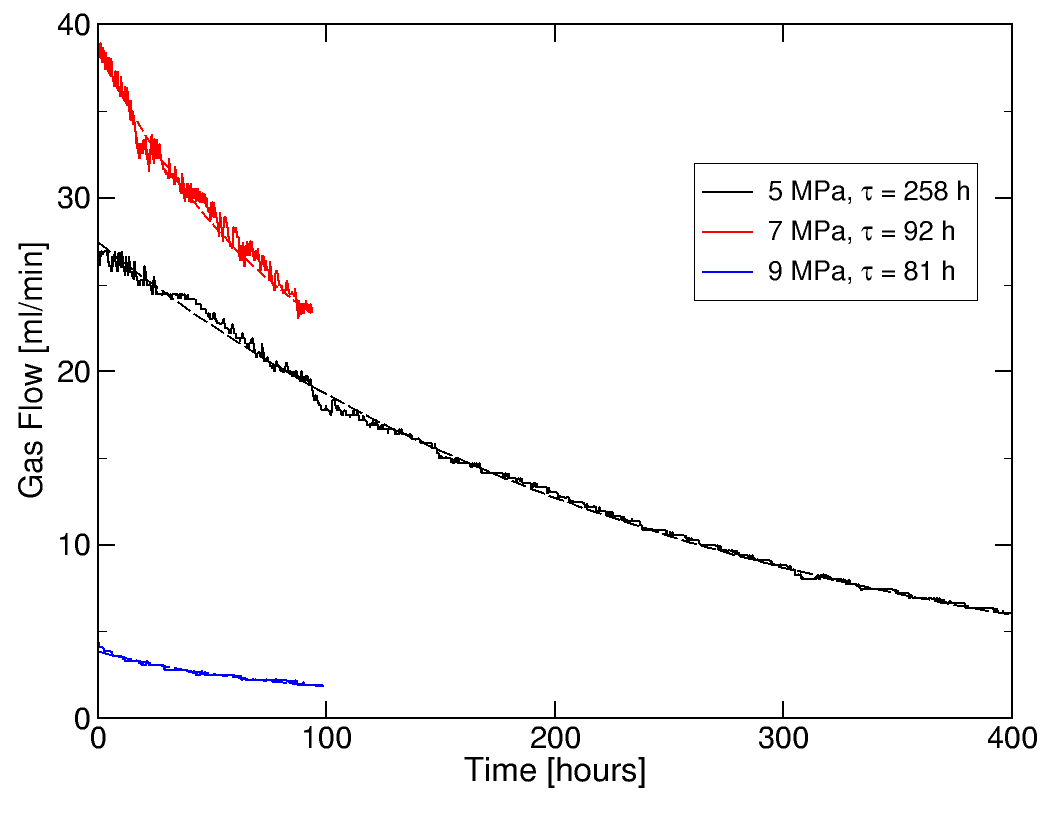
Experiment: Closure and healing of cracks in Opalinus clay
We conducted experiments on samples of the sandy facies of Opalinus clay, to study the long term behavior of cracks under isostatic stress conditions. It turned out that the clay was so fragile, that already the preparation of the samples induced enough microscopic damage to measure a significant permeability. A gas pressure of 0.5 bar was applied to one side of the probe, and the gas flow was measured for several days under various stresses. The decay rates agree with the expectation, that the closures take place faster under higher stresses.
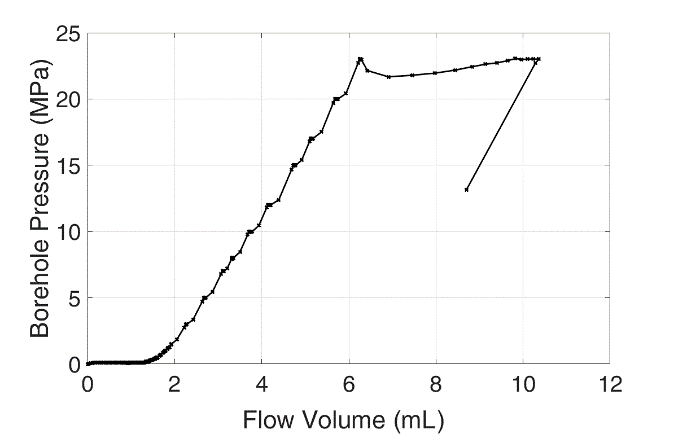
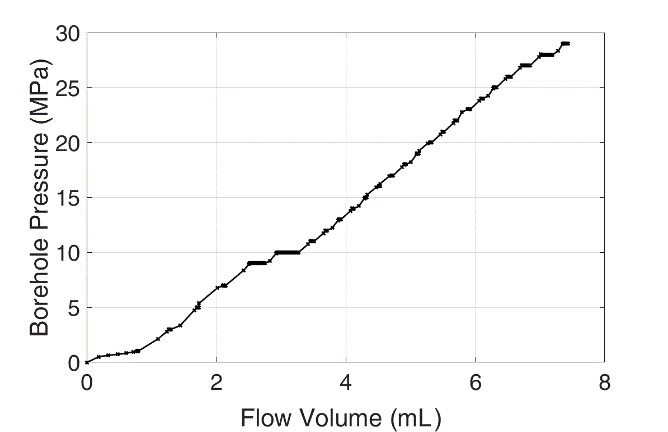
In the geotechnical/geomechnical laboratory of CAU Kiel, the fluid driven percolation tests are performed. The cubic Opalinus claystone samples are prepared in the side dimension of 43 mm and with the drilled cavity length and diameter of 20 and 8 mm, respectively. The samples embedded layering orientations are shown in Fig. 1, where in the first case the applied oil pressure is perpendicular to the layering orientations and in the second case it is parallel to the layering orientations. The syringe pump is used to pump the pressurized hydraulic oil (up to 517 Bar) into the sample and with gradually increasing the pressure the fracking process is carried out. In the first setup, the hydraulic fracking is initiated at 23 MPa and the clear flow paths through the embedded layering surfaces is observed. similarly, for the second test setup, the hydraulic fracking is initiated at 10 MPa through the embedded layering surfaces. Fig. 2 illustrates the borehole pressure evolution with flow volume change obtained from the experimental data. The initial volume of the pump is around 265 mL.


(a) (b)
Fig. 1. The fracking paths through the Opalinus claystone for a (a) 1st stress, and (b) 2nd stress configuration
(a) (b)
Fig.2. The borehole pressure vs. flow volume for an Opalinus claystone (a) 1st stress configuration, and (b) 2nd stress configuration
CAU Kiel
The fluid-driven percolation experiments on cubical clay and salt samples with dimensions of 43 x 43 x 43 mm are conducted under laboratory conditions at CAU Kiel. The hydraulic pump filled with hydraulic oil can reach a pressure of up to 700 bar. The pressure-controlled technique is considered, and the corresponding flow rates are stored. Three samples under different stress boundary conditions undergo the fracking process using the true triaxial apparatus. The existing P and S-wave ultrasonic sensors on pistons are used to measure the material property change using the analytical relation existing in literature. According to the pre-existing mechanical stress distribution, the fracking pattern under applied hydraulic pressure is unique for each stress distribution. In order to visualize the fracking path, X-Ray computed tomography (XRCT) scans are made at the University of Stuttgart from samples before and after fracking. To keep the cracks open, a mixture of metal powder with a maximum particle dimension of 30 micrometers is added to the fluid mixture.
 Fig. 1: The pump used for applying the hydraulic pressure (left), the preparation of the sample in the true triaxial apparatus (right, top), and the prepared cubic sample with the drilled cylindrical cavity (right, bottom)
Fig. 1: The pump used for applying the hydraulic pressure (left), the preparation of the sample in the true triaxial apparatus (right, top), and the prepared cubic sample with the drilled cylindrical cavity (right, bottom)
IfG
Modelling: Shrinking of clay and crack opening due to desiccation
When clay is exposed to air, for example on the surface of walls of drifts, it tends to develop cracks because its water content evaporates. The pore pressure in the material is reduced, leading to tensile stresses which eventually open up cracks. Recently, Itasca added a feature of bulk pore pressure to its 3DEC program in addition to the usual discrete element fluid knot feature, which could open up the possibility to model and analyze such processes. We are currently exploring the possibility by simulating a block of saturated clay with a constant evaporation rate at the top. As expected, we see the creation of cracks:
 Fig. 2: Opening of cracks (color-coded displacement magnitude) on a block of clay because of evaporation of water
Fig. 2: Opening of cracks (color-coded displacement magnitude) on a block of clay because of evaporation of water
Up to now, only qualitative results have been obtained. It remains to be explored whether the model is also able to function with more realistic parameter sets.
At CAU Kiel, the gas and fluid pressure-driven percolation in clay and salt stones are experimentally and numerically investigated. Using the true triaxial device in the laboratory of CAU Kiel, a fluid-driven percolation test on a cubic sample is carried out. By controlling the three principal stresses individually, the frack paths and change of flow rate are determined.
 Fig. 1: The prepared cubic claystone sample (43 x 43 x 43 mm) (left) and the true triaxial device (right)
Fig. 1: The prepared cubic claystone sample (43 x 43 x 43 mm) (left) and the true triaxial device (right)
The crack initiation and propagation, change of permeability, change of flow rate upon cracking and during the healing process and developed frack paths are all captured with the hydro-mechanical dual lattice model (Grassi 2009). The conduct elements are the fluid pathways throughout the discretized medium.
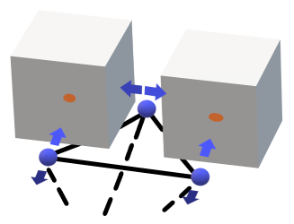 Fig. 2: The conduct elements shown with black lines
Fig. 2: The conduct elements shown with black lines
 Fig. 3: The 3D Hydro-mechanical LEM simulation of fluid-driven percolation is salt stone. The fracking surfaces are shown in red (left) the developed water pressures in the medium (right)
Fig. 3: The 3D Hydro-mechanical LEM simulation of fluid-driven percolation is salt stone. The fracking surfaces are shown in red (left) the developed water pressures in the medium (right)
P. Grassl (2009). A lattice approach to model flow in cracked concrete. Cement & Concrete Composites 31 (2009) 454–460.
Experiments on Pressure-driven Percolation and Sealing/Healing of cracks
Up to now, three experiments have been carried out to study the sealing and healing of cracks in rock salt. Boreholes were drilled to the center of cylindrical samples and fitted with a metal pipe so that gas pressure could be applied to a small area at the center.


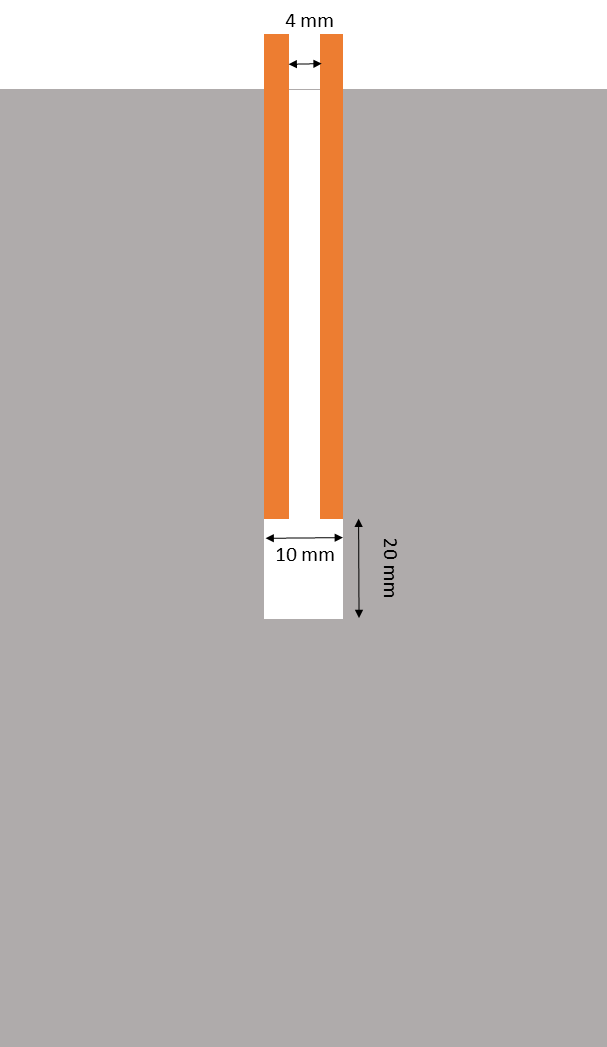
Initially, all samples were placed under isostatic stress of 50 MPa for one day to consolidate them. For the actual experiments, the isostatic stresses were then changed to 10 MPa, 30 MPa, and 50 MPa, respectively. A gas pressure at the center of the samples was then applied and increased in small steps until a gas flow was detected. In all three cases, a gas flow was detected before the percolation threshold was reached (usually a few bar below), which indicates that the samples suffered micro-fractures during preparation. After the last increase of the pressure, the flow rate was monitored for 24 to 60 hours under constant conditions. The corresponding permeabilities were:
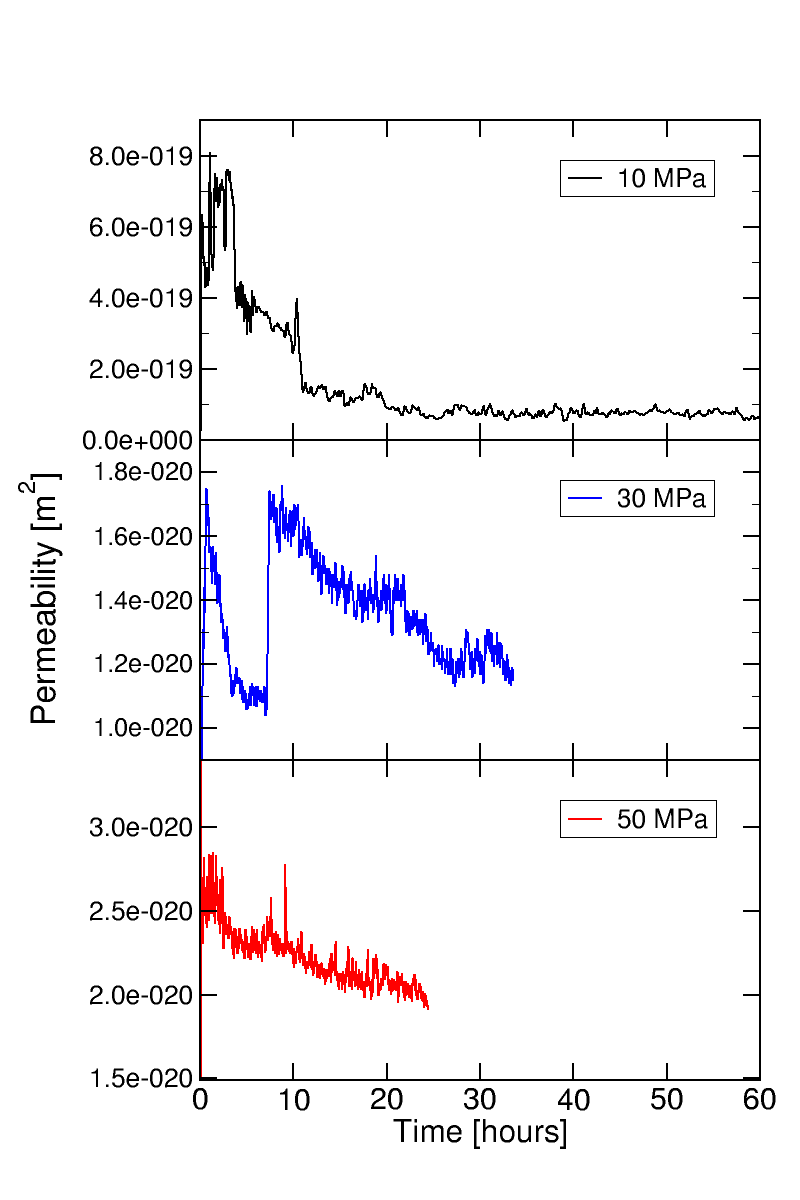
In all three cases, a reduction of the permeability was observed, showing a narrowing of the pathways due to creep.
Further analysis and a numerical model for WP 2.2 (see following article: Numerical Model of Fractures) are work in progress.
Numerical Modeling of Fractures
The IfG worked on several Model Exercises (ME) that were agreed on between the project partners of GeomInt.
The first ME was a simple three-point bending test to compare how the various methods employed at the different institutions describe fracture mechanics. We used the discrete element method 3DEC (Itasca Consulting Group) to set up two models of a granite bar:

For each, the force and the crack mouth opening displacement (CMOD) were recorded as well as the acoustic emissions.
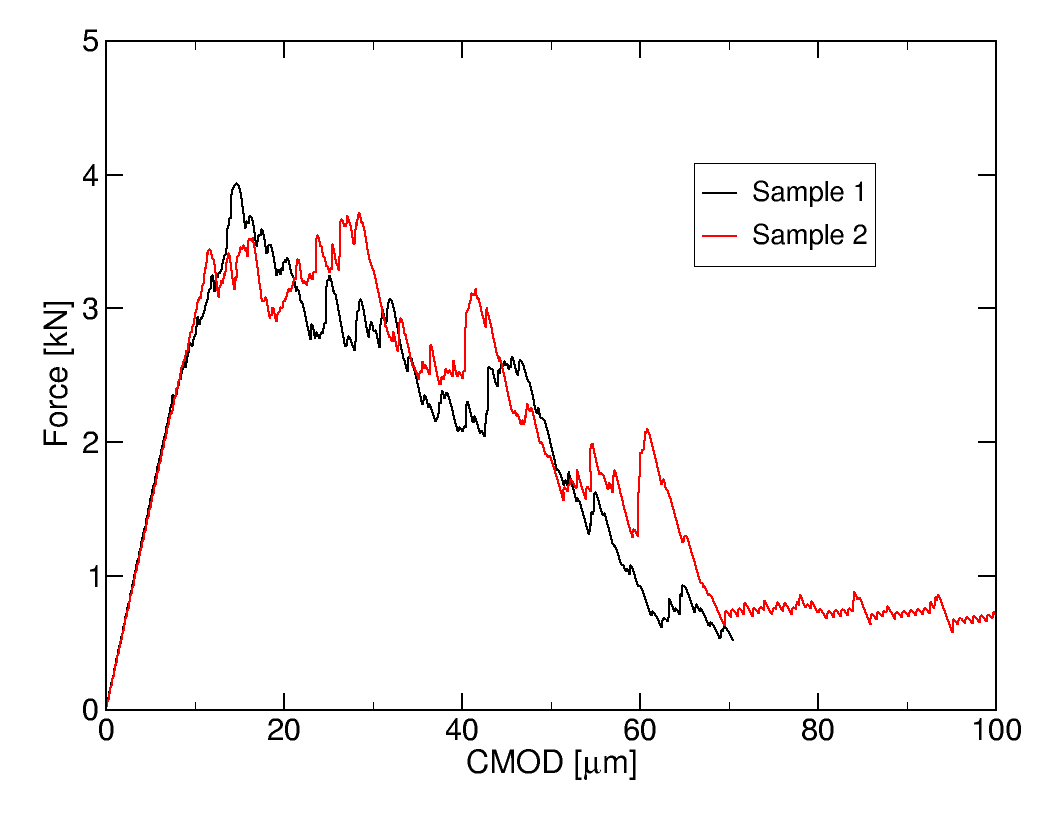 Force-CMOD behaviour for the two samples
Force-CMOD behaviour for the two samples
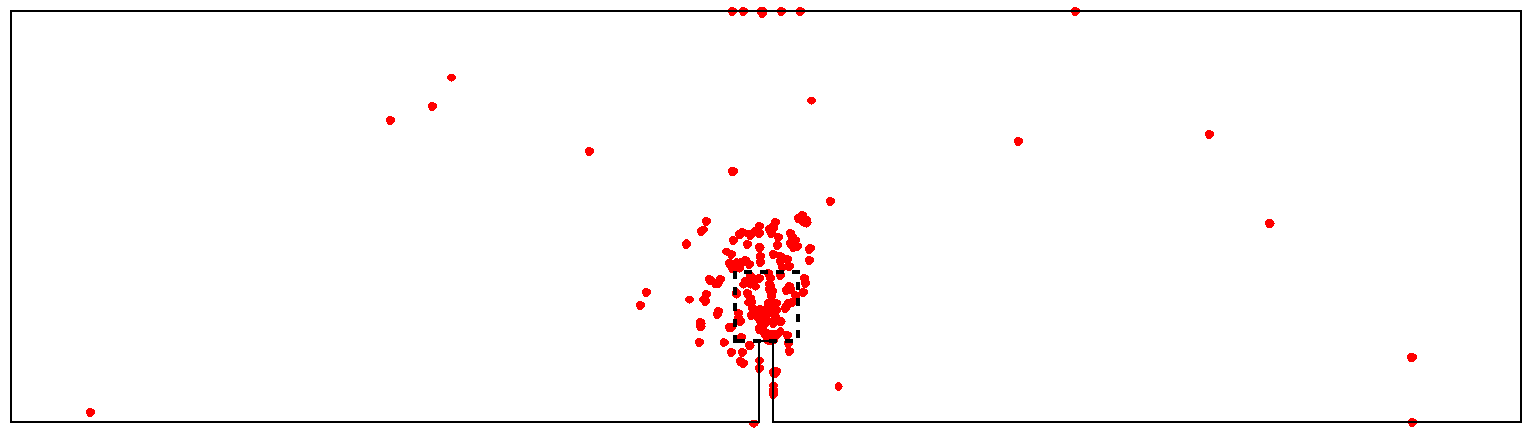 Locations of acoustic emissions for the first sample
Locations of acoustic emissions for the first sample
The results agree very well with an experiment done by Tarokh et al. (Int. J. Fract. 204, p 191 (2017)).
In a second ME, pressure-driven percolation in a cubic sample of rock salt in an anisotropic true-triaxial stress state was simulated. The purpose was to study the orientation of the resulting fractures as a function of the stress state and to compare the performance of the various methods employed by the project partners. Here again we used 3DEC:
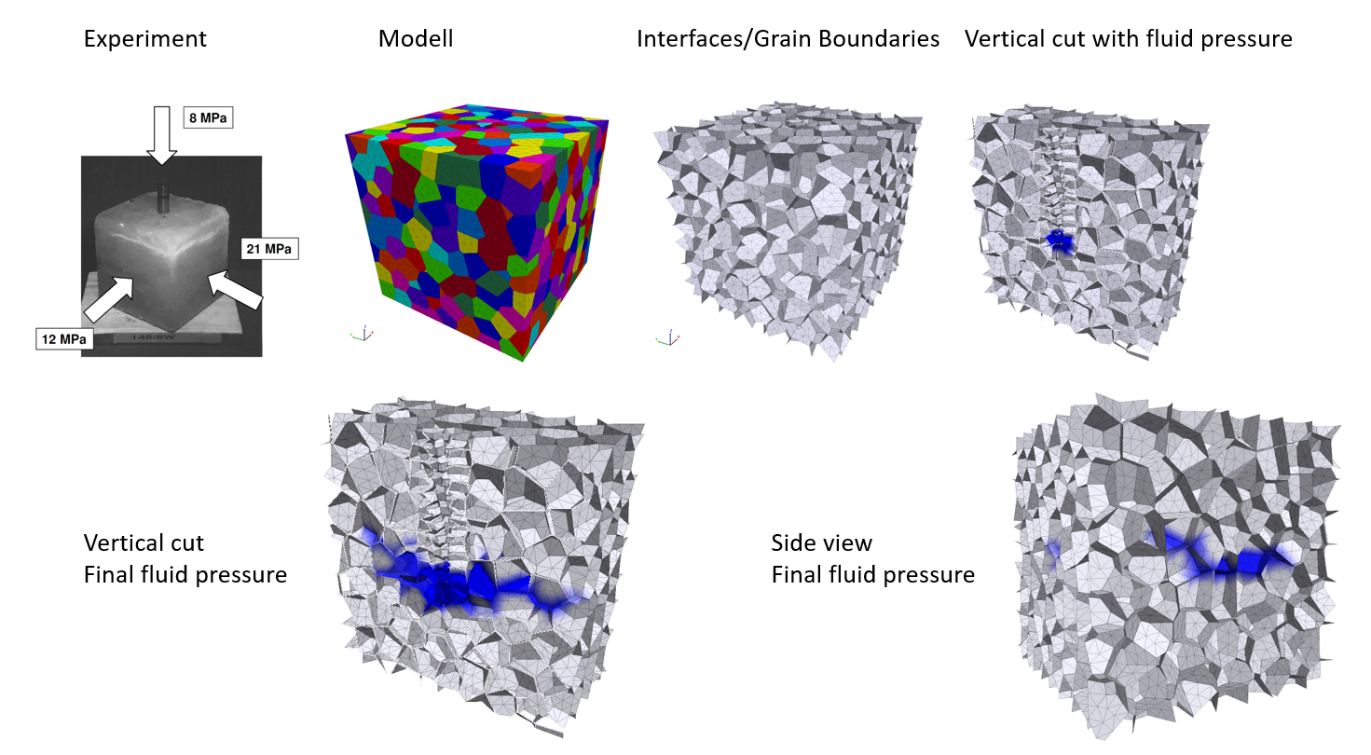 Left: Experimental situation, right: Model results. As the minimal principal stress is in the vertical direction, a horizontal frac is produced.
Left: Experimental situation, right: Model results. As the minimal principal stress is in the vertical direction, a horizontal frac is produced.
 Left: Experimental situation, right: Model results. As the minimal principal stress is in the horizontal direction, a vertical frac is produced.
Left: Experimental situation, right: Model results. As the minimal principal stress is in the horizontal direction, a vertical frac is produced.
IfG
Development of numerical methods: Quantitative treatment of pressure driven percolation and the difference between liquids and gas
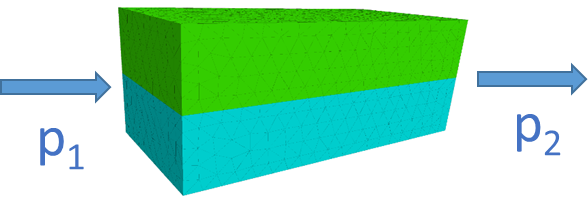 Simple model system
Simple model system
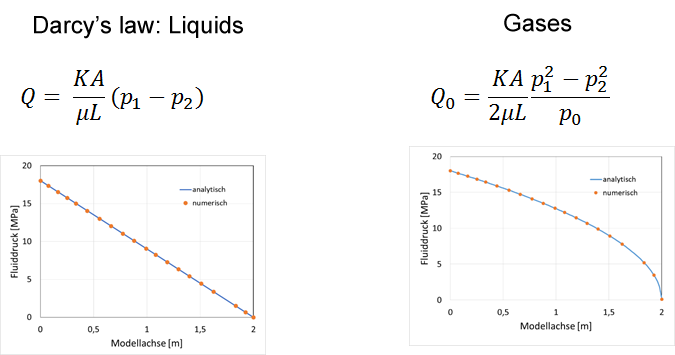 Pressure profiles
Pressure profiles
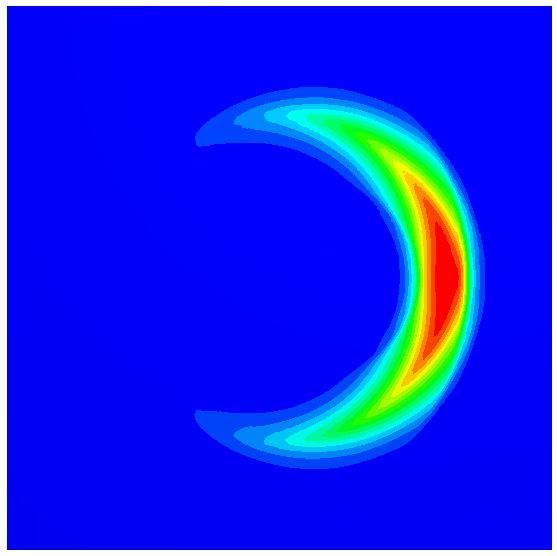
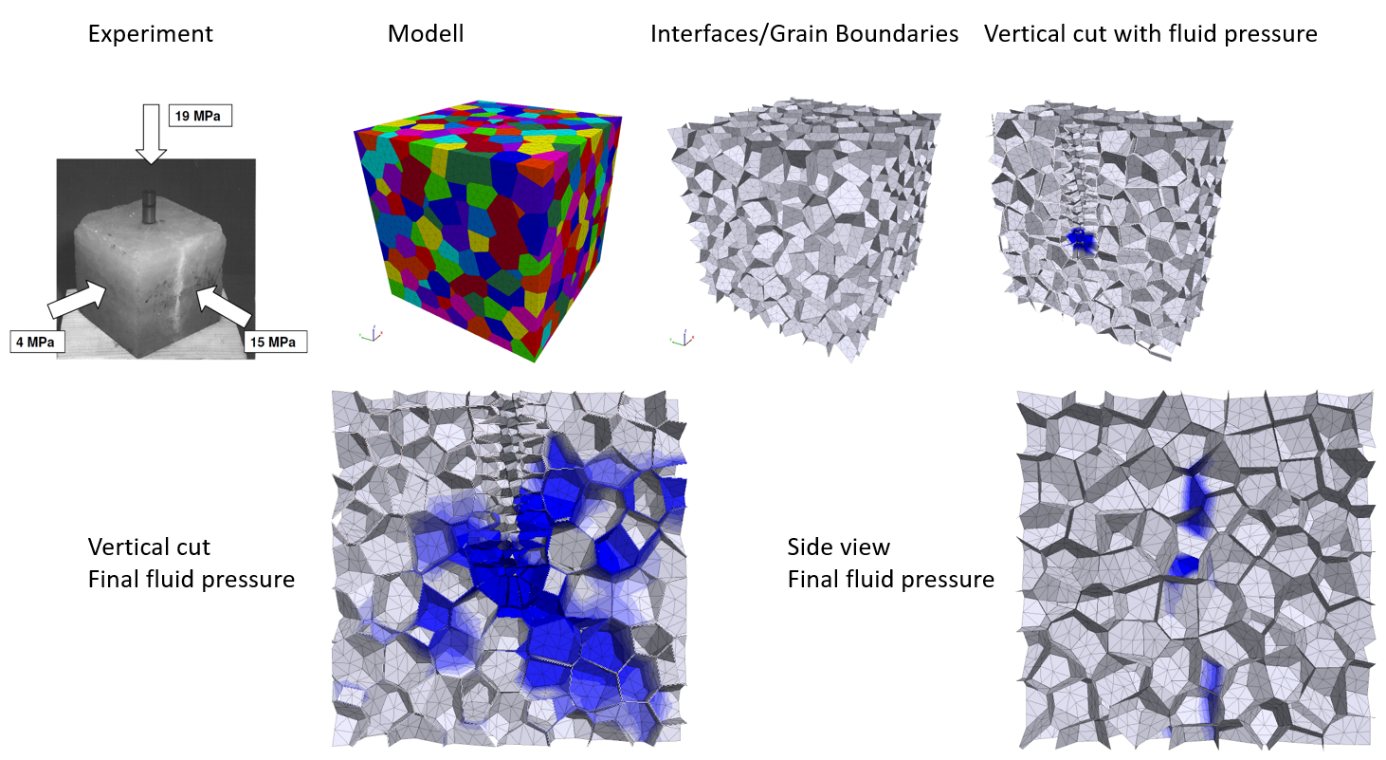
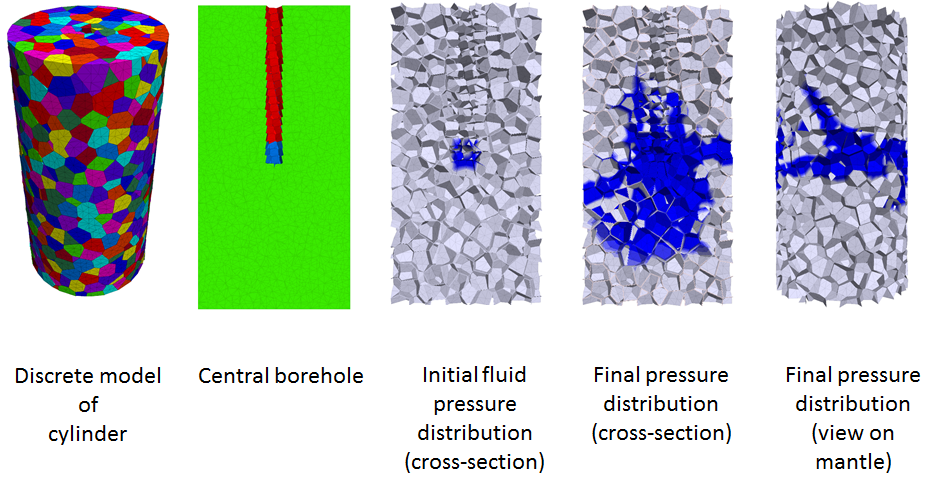
Pressure-driven percolation in a cylindrical sample: In a homogeneous sample and stress state, the fluid expands in an isotropic pattern.
BGR
BGR has tested the implementation of the new implemented X-FEM LIE approach in OGS-6. With this approach, it is possible to simulate the hydraulic stimulated deformation behavior of an existing crack. This includes opening and closing, shear deformation and change of crack permeability.
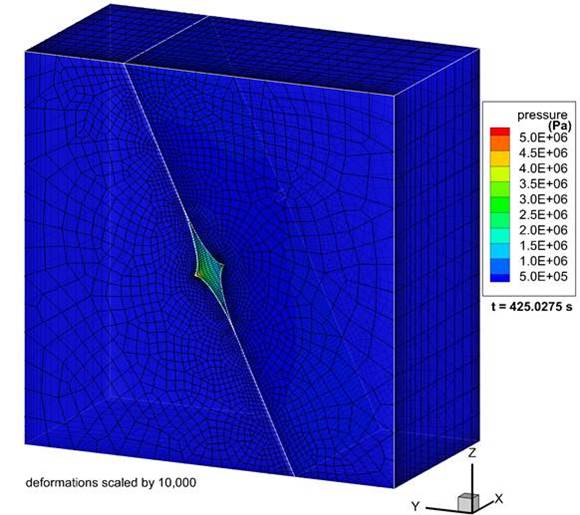 Exemplary calculation of crack deformation, induced by fluid injection. Simulated with OGS-6.
Exemplary calculation of crack deformation, induced by fluid injection. Simulated with OGS-6.
In order to determine the flow pathways through pressure-driven percolation, the experimental result provided from our project partner IfG Leipzig is used. In their provided test a cylindrical sample is under radial confinement pressure of 50 MPa and gas pressure is gradually increased till the gas flow rate initiated in the medium (Figure 1).
 Figure 1: The cylindrical sample and cutoff to apply gas pressure and observe the change of flow rate with fracture propagation (IfG Leipzig)
Figure 1: The cylindrical sample and cutoff to apply gas pressure and observe the change of flow rate with fracture propagation (IfG Leipzig)
With application of lattice element method (LEM) and using the dual lattice method to define the conduct elements as flow paths (Lij), the hydro model is coupled with previously developed mechanical model.
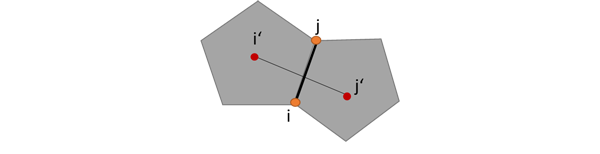 Figure 2: The dual lattice model for coupled hydro-mechanical lattice model
Figure 2: The dual lattice model for coupled hydro-mechanical lattice model
The gas flow rate change with developed pressures and fracture aperture is determined using,
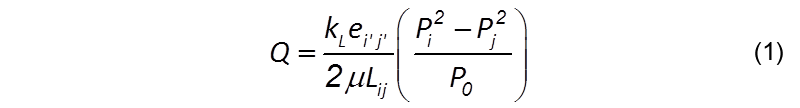
where kL is the permeability, ei’j’ is the aperture width in 2D lattice model, Lij is the conduct element length, μ is the viscosity and Pi and Pj are the gas pressure in i and j conduct points.
According to the differential equation of the non-stationary flow problems, the flow in a single conduct element (i,j) is,
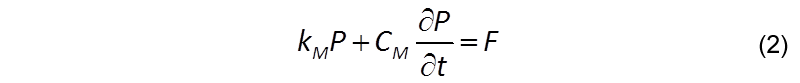
where kM and CM are the conductivity and capacity matrix, respectively and P is the pressure potential with two degrees of freedom.
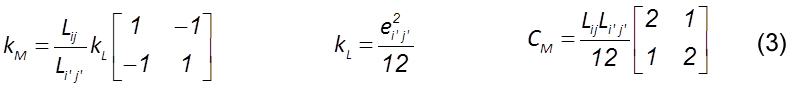
With solving the aforementioned equation the applied forces on conduct points (i,j) as well as lattice points (i‘,j‘) are determined and inserted in mechanical model. The change of aperture width, ei’j’, with crack opening is determined and transferred to flow model. The LEM boundary condition is shown in figure 3. The generated lattice model has 20,000 Voronoi cells and randomness factor of 0.5. The model has around 50,000 elements. The fracture flow path in the tip of the hole is shown in Figure 4. In general, the fracture pathway is in horizontal direction.
The comparison of experimental results from IfG Leipzig and LEM simulation results from CAU Kiel is shown in Figure 5. The fracture initiation is at gas pressure of 39.6 MPa, which corresponds to propagation of gas flow into medium. In LEM, the gas pressure is gradually increased, 0.1 MPa steps, till 45 MPa. The healing of the fractures is not captured with LEM, which need to be investigated.
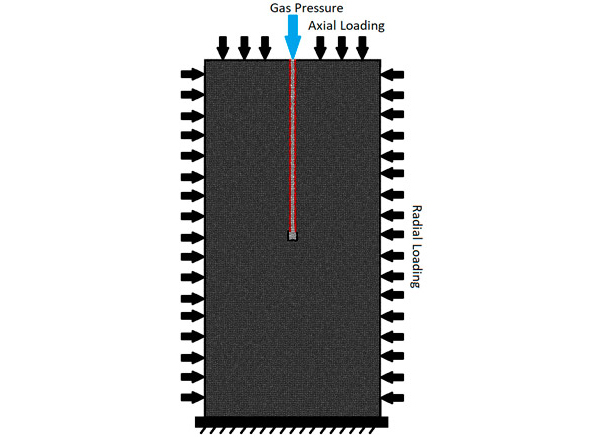 Figure 3: The LEM boundary condition for simulation of pressure-driven percolation
Figure 3: The LEM boundary condition for simulation of pressure-driven percolation
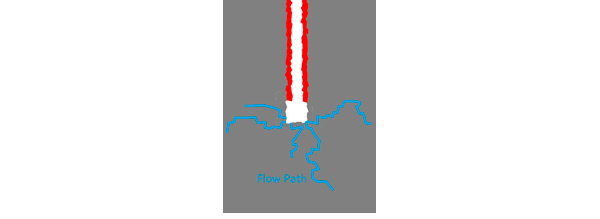 Figure 4: The LEM result of flow pathway in saltstone under pressure-driven percolation
Figure 4: The LEM result of flow pathway in saltstone under pressure-driven percolation
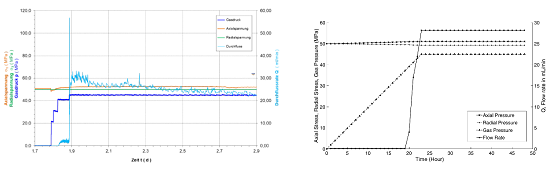 Figure 5: Comparison of experimental and LEM simulation results of pressure-driven percolation in cylindrical saltstone.
Figure 5: Comparison of experimental and LEM simulation results of pressure-driven percolation in cylindrical saltstone.
The IfG set up a three-dimensional model to test several approaches for the propagation of fluids by pressure driven percolation. Pressure driven percolation is defined as the opening of intercrystalline grain boundaries, caused by fluid pressure, that leads to the creation of interconnected flow paths. A library of subroutines has been set up, with several numerical functions that can describe the advancement of the fluid front. Currently numerical simulations are under way to study the influence of the compressibility of the fluid, with a focus on the difference between gases and liquids.
Within AP2, the UFZ team implemented cohesive zone models for hydraulically stimulated fracturing as well as specific hydraulic fracture flow laws into numerical methods in OpenGeoSys using enriched finite element spaces. Simultaneously, a phase field model for pressure driven pathway generation has been implemented and is being tested.
Currently, comparisons between both methods are ongoing regarding the quantification of key physical quantities such as fracture volume or percolation/fracture initiation pressure.
The flow path in salt stones is due to pre-existing or developed discontinuities in the microstructure. The mechanical loads can result in new flow paths as well as propagation of pre-existing microcracks and eventually increase of the hydraulic conductivity of the salt stones. In this regard, in CAU Kiel laboratory, extensive experimental tests under coupled thermo-hydro-mechanical (THM) conditions will be conducted. The aim is to investigate the change of THM property of salt stones due to developed microcracks. Besides the laboratory tests, the numerical study is also conducted. While using in-house developed Lattice Element Method (LEM) and the experimental results, a new numerical method for determining the change of hydraulic conductivity under THM processes will be developed. According to our research results in CAU Kiel, the developed LEM is able to capture the developed fracture path and it‘s effect on mechanical and thermal properties of the rock samples.
 Figure 1: The transform of (a) microscopic image of cemented rock material into (b) developed lattice element while using the image processing toolbox of MATLAB. [1]
Figure 1: The transform of (a) microscopic image of cemented rock material into (b) developed lattice element while using the image processing toolbox of MATLAB. [1]
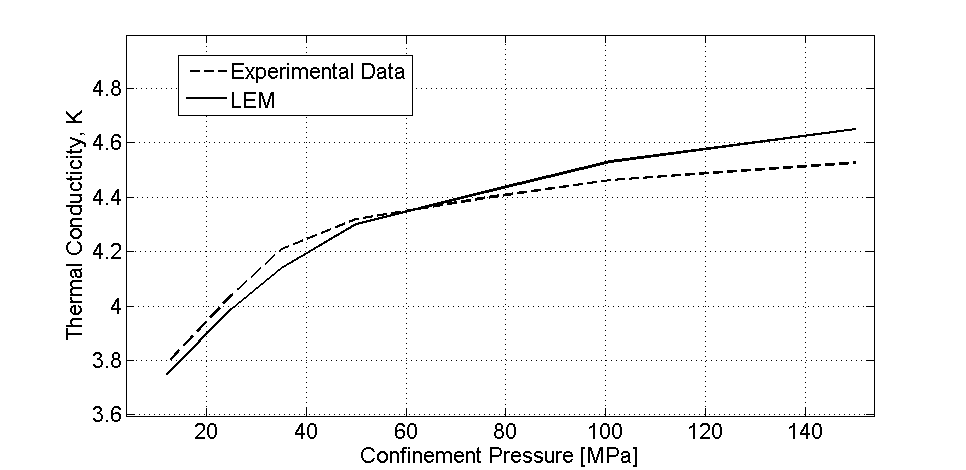 Figure 2: The comparison of the determined experimental thermal conductivities of rock sample (Fig 1) with LEM while applying different confinement pressures. [1]
Figure 2: The comparison of the determined experimental thermal conductivities of rock sample (Fig 1) with LEM while applying different confinement pressures. [1]
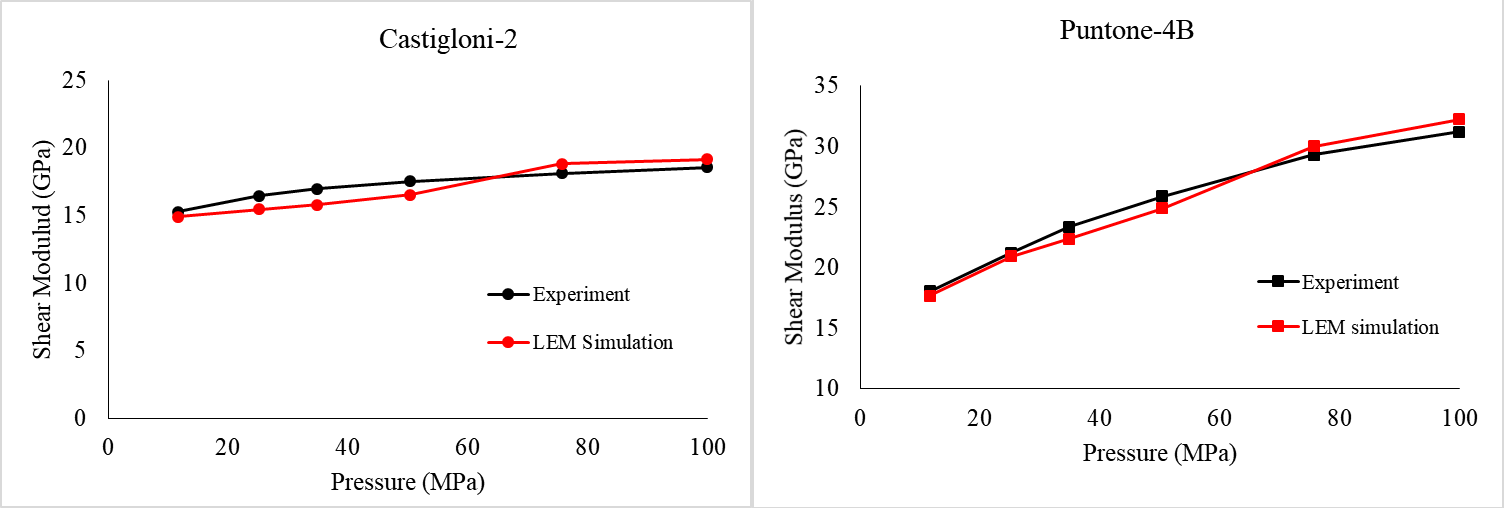 Figure 4. Variation of shear moduli of two rock samples at 20°C with the change in applied hydrostatic pressure up to 101 MPa. The local elemental failure is considered and the thermal strain is not considered for the failure. [2]
Figure 4. Variation of shear moduli of two rock samples at 20°C with the change in applied hydrostatic pressure up to 101 MPa. The local elemental failure is considered and the thermal strain is not considered for the failure. [2]
References:
[1] A. S. Sattari, Z. H. Rizvi, H. B. Motra, F. Wuttke (2017). Meso-scale modeling of heat transport in a heterogeneous cemented geomaterial by lattice element method. Granular Matter. 19:66. (DOI 10.1007/s10035-017-0751-4).
[2] Zarghaam H. Rizvi, Amir S. Sattari, Hem B. Motra, Frank Wuttke (2017). Effective parameter evaluation in heterogeneous cemented geomaterials subjected to high temperature, pressure and constrained deformations, Second International Symposium on Coupled Phenomena in Environmental Geotechnics, University of Leeds, UK.
