Main research areas

Assembly and dynamics of plant communities
In the early 1990’s I started my Postdoc work with the objective of analyzing the complex, event-driven dynamics of semiarid plant communities in the Karoo, South Africa (e.g., Wiegand et al. 1995, 1998a). To this end I developed methods of bottom-up simulation modeling, extending earlier work on cellular automata. My models were able to describe the spatial and temporal dynamics of several interacting species. Nowadays, these models are frequently used in ecology. Understanding the assembly and dynamics of plant communities remains one of my main research themes; it was also the core question of my ERC advanced grant SpatioDiversity where we mostly analyzed tropical forest communities (e.g., Kazmierczak et al. 2014; May et al. 2015, 2016, 2020; Wiegand et al. 2017a, 2021), and is the focus of the ERC advanced grant SpatioCoexistence. However, my lab applies these techniques also to other systems such as semiarid plant communities (Cipriotti et al. 2012, 2014, 2016, 2019) and treelines (Wiegand et al. 2006a; Martinez et al. 2011; Bader et al. 2021)

Spatiotemporal dynamics of animal populations
In the early 2000’s I became interested in reconciling the perspectives of landscape ecology and population modeling to better understand the spatiotemporal dynamics of endangered animal populations such as those of brown bears (Wiegand et al. 1998a, 1999, 2008), lynx (Schadt et al. 2002, Kramer-Schadt et al. 2005; Revilla and Wiegand 2008), koala (Rhodes et al. 2006), woodpecker (Bruggeman et al. 2010, 2014), tiger (Kanagaraj et al. 2011, 2013), jaguar (De Angelo et al. 2013), albatross (Louzao et al. 2011, 2013, 2014), tortoise (Anadón et al. 2012; Graciá et al. 2020; Jiménez-Franco et al. 2020, 2022, 2024) or lizards (Rodríguez-Pérez et al. 2012a,b), especially under habitat loss and fragmentation.
This approach to spatially explicit population modeling rests on three steps. In a first step the landscape must be defined as perceived by the species of interest. This is accomplished with statistical methods of species distribution modeling where the presence/absence/abundance of the species is statistically related to environmental variables that are often based on remote sensing data.
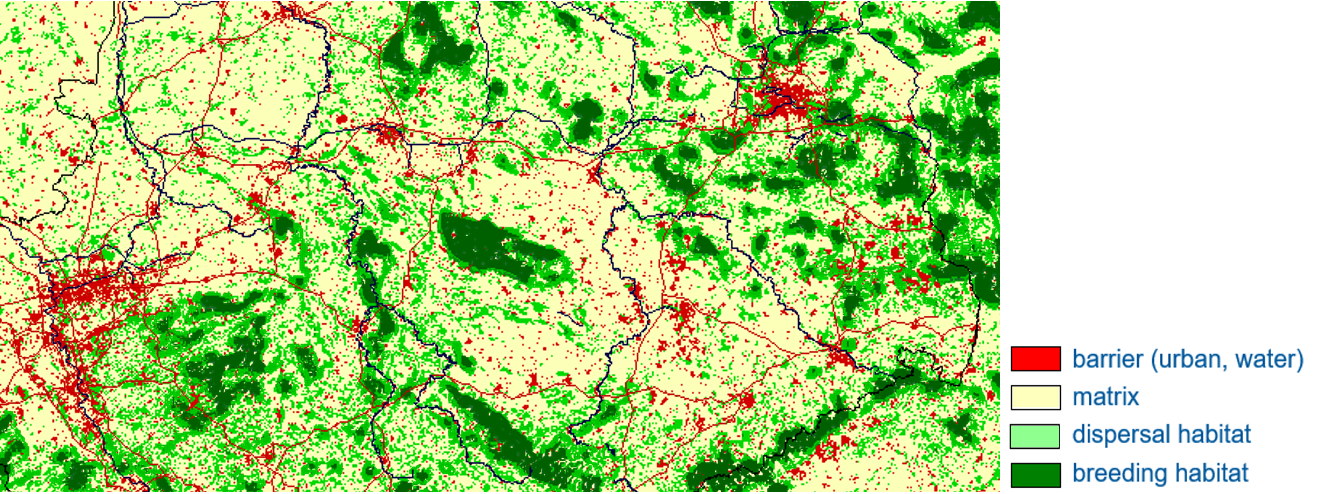
In a second step, an individual-based movement model that simulated the dispersal of juveniles in the landscape defined in the first step in search of own territories or home ranges. These are often random-walk type models, which can include autocorrelation, habitat bias or a homing behavior (e.g., Anadon et al. 2012; Bruggeman et al. 2014). They can be used to assess e.g., patch connectivity or effects of street mortality. An especially interesting application of movement models in real landscapes is to study animal seed dispersal (Fedriani et al. 2018; 2020). Finally, a complete demographic (age-or stage-structured) model is added in the third step to study various aspects population or metapopulation dynamics (Wiegand et al. 2004; Revilla and Wiegand 2008; Gracia et al. 2020; Jimenez-Franco et al. 2020, 2022, 2024).
Methods of model-data integration
During my work on spatially-explicit simulation models and endangered species it became obvious that existing modeling strategies were insufficient to face the two main challenges of bottom-up modeling: complexity and uncertainty. I also realized that in most cases only a small fraction of the available data have been used to address fundamental questions related to the emergence, consequences, and conservation of global biodiversity. To advance our ability of model-data integration I further developed the inverse pattern-oriented modeling strategy that allows using multiple observed patterns typically encoded in large and complex data sets. This method allows for statistical inference with dynamic and stochastic simulation models that incorporate the required real world ecological complexity.
In other fields these methods are termed Approximate Bayesian Computation (ABC) and are extensions of statistical methods of model fitting and model selection that allow testing competing hypotheses, inclusion of data from different sources and hierarchical levels, and observer bias (i.e., a virtual ecologist). Key publications are Wiegand et al. (1998a, 2003, 2004), Grimm et al. (2005), Hartig et al. (2011, 2014), Martínez et al. (2011, 2016), Anadon et al. 2012; Cipriotti et al. 2012, and May et al. (2015, 2016).

Spatial point pattern analysis
To analyze the spatially-explicit outputs of my simulation models of plant communities (Wiegand et al. 1998b), I became interested in spatial pattern analysis. To this end I developed the software Programita that is based on many years of teaching experience and collaborative research with field ecologist and especially designed to meet the “real world” requirements of ecologists. My work on spatial point pattern analysis and the software Programita has initiated in ecology a new and productive line of thinking in the analysis of spatial data. In 2004 I summarized the state-of-the-art in point pattern analysis in Ecology in a Mini review in Oikos (Wiegand and Moloney 2004) and 10 years later we published a textbook on point pattern analysis in ecology ( Wiegand and Moloney 2014 ). The review by Velazquez et al. (2016) summarizes the use of point pattern analysis in ecology, and the review paper Wiegand et al. (2017b) summarizes more recent advances where spatial point pattern analysis is combined with phylogenetic and trait analysis (see also Shen et al. 2013; Wang et al. 2016).
I have applied spatial point pattern analysis in my own research in numerous studies to precisely describe spatial patterns in ecological communities for hypothesizing underlying processes or for testing ecological hypotheses. Detailed spatial pattern analysis of forest communities was one of the three columns of my first ERC advanced grant. Recently I became interested in marrying spatial point pattern analysis with dynamic population and community modeling to derive a spatially explicit coexistence theory (Wiegand et al. 2021). This is the focus of my second ERC grant SpatioCoexistence.
Integration of spatial point pattern analysis with dynamic models
For many years I have studied and quantified the detailed features of spatial patterns in plant communities (e.g., Wiegand et al. 2007, 2009, 2012, 2017b, Perea et al. 2021, 2022, Muñoz-Gallego 223a, b, Salazar Villegas et al. 2023), and we have used spatial patterns in inverse pattern-oriented approach for parameterization and model selection in stochastic simulation models (e.g., Martinez et al. 2011; May et al. 2015, 2016). However, a key question in ecological theory, namely how spatial patterns influence community dynamics and coexistence, has remained largely unanswered. Should the information hidden in spatial patterns, such as that shown by data of the Smithsonian ForestGEO network, convey information on the underlying ecological mechanisms or even hide the key to coexistence?
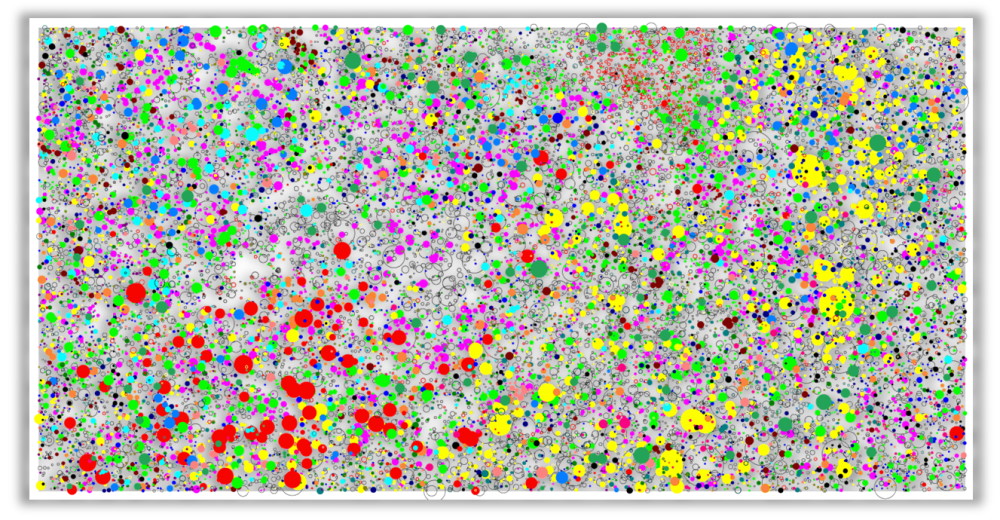 Map showing for the 50-ha plot of tropical forest at Barro Colorado Island all trees with a diameter at breast (dbh) high larger than 10cm, with the diameter of the circle being proportionally to dbh. Only the 29 most common species were coloured, all other individuals are represented by black circles.
Map showing for the 50-ha plot of tropical forest at Barro Colorado Island all trees with a diameter at breast (dbh) high larger than 10cm, with the diameter of the circle being proportionally to dbh. Only the 29 most common species were coloured, all other individuals are represented by black circles.
For example, if spatial patterns alone could stabilize species rich communities of ecologically very similar species, a new type of spatial coexistence theory would be possible that overcomes the limitations imposed by Gause’s non-spatial exclusion principle and opens up exciting new avenues to explain the paradox of species rich communities.
In Wiegand et al. (2021) we outlined such a spatial coexistence theory. The biggest obstacle to overcome was a scaling issue, i.e., to find a way to translate the relevant “microscopic” detail of the emerging spatial patterns into a “macroscopic” mathematical coexistence theory. We solved this issue by deriving transfer functions that express the population-level interaction coefficients of macroscopic models in function of several indices of spatial point pattern theory, which involve different levels of interactions: intraspecific clustering, interspecific segregation and the mean interaction strength of a heterospecific neighbor.
We found that, to obtain positive abundances, all species must show similar values of a “feasibility” index resulting from our theory. This index describes a demographic balance leading to coexistence where no species gains an advantage over others. It allows species to differ in many ways, as long as they keep the overall demographic balance.
Deeper analysis showed that the spatial simulations exhibit rather complex dynamics with two different dynamical regimes, a stable regime characterized by a demographic balance governed by the feasibility index, and a regime of “neutral stability” where the individual species abundances follow a stochastic random walk, but total community size approaches equilibrium. The unstable regime arises if tree recruitment takes place mostly close to the parent trees (as typically modeled by a kernel function), whereas the stable regime can arise if recruitment is clustered, but spatially independent of the parent trees, as e.g., caused by animal seed dispersal or canopy gaps.
Much of my current work, including the ERC advanced grant SpatioCoexistence, involves now generalizing the research program opened up Wiegand et al. (2021). Next steps are inclusion of more biological details to place the spatial coexistence mechanism in perspective of other mechanisms. The direct link of the spatial theory to spatial patterns provides access to the rich source of data to validate spatial simulations of alternative models against multiple biodiversity patterns.
See also my blog to the paper.
References
- Anadón, J.D., Wiegand, T. and A. Giménez.2012. Hypothesis testing with individual-based movement models reveals sex-biased effects of landscape fragmentation on movement patterns of a terrestrial tortoise. Ecosphere 3: 64.
- Bader, M., Llambí, L.D., Case, B., Buckley, H., Toivonen, J., Camarero, J.J., Cairns, D., Brown, C., Wiegand, T., and L. Resler. 2021. A global framework for linking alpine-treeline ecotone patterns to underlying processes. Ecography 44: 265 – 292
- Bruggeman, D. J., T. Wiegand, and N. Fernández. 2010. The relative effects of habitat loss and fragmentation on population genetic structure. Molecular Ecology 19: 3679–3691
- Bruggeman, D.J., T. Wiegand, J. R. Walters, F. Gonzalez Taboada , K. Convery. 2014. Contrasting the ability of data to make inferences regarding dispersal for the Red-cockaded woodpecker (Picoides borealis). Landscape Ecology 29: 639-653
- Cipriotti, P.A., M.R.Aguiar, T, Wiegand, and J. M. Paruelo. 2012. Understanding the long term spatial dynamics of semiarid grass shrub steppes through inverse parameter selection for simulation models. Oikos 121: 848- 861
- Cipriotti, P.A., M.R.Aguiar, T. Wiegand, and J. M. Paruelo. 2014. A complex network of interactions controls coexistence and relative abundances in Patagonian grass–shrub steppes. Journal of Ecology 102: 776 - 788
- Cipriotti, P.A., T. Wiegand, S., Pütz, N.J., Bartoloni, and J.M. Paruelo. 2016. Non-parametric upscaling of stochastic simulation models using transition matrices. Methods in Ecology and Evolution 7: 313-322.
- Cipriotti, P.A., M.R. Aguiar, T. Wiegand, and J. M. Paruelo. 2019. Combined effects of grazing management and climate on semi-arid steppes: hysteresis dynamics prevent recovery of degraded rangelands? Journal of Applied Ecology 56: 2155-2165
- Cipriotti, P.A., S. Pütz, J.M. Paruelo, N.J. Bartoloni, and T. Wiegand. 2023. A systematic strategy to analyze individual-based models reveals pathways of degradation and recovery in Patagonian rangelands. Oikos 12 e09999
- De Angelo, C., A. Paviolo, T. Wiegand, R. Kanagaraj and M. S. Di Bitetti. 2013. A management landscape for jaguars in the Upper Paraná Atlantic Forest. Biological Conservation 159: 422–433
- Fedriani, J.M., T. Wiegand, D. Ayllón, F. Palomares, A. Suárez-Esteban, and V. Grimm. 2018. Assisting seed dispersers to restore old-fields: an individual-based model of the interactions among badgers, foxes, and Iberian pear trees. Journal of Applied Ecology 55: 600-611
- Fedriani, J.M., D. Ayllón, T. Wiegand, and V. Grimm. 2020. Intertwined effects of defaunation, increased tree mortality, and density compensation on seed dispersal. Ecography 43: 1352-1363.
- Graciá, E, R. Rodríguez-Caro, A. Sanz-Aguilar, J. Anadón, F. Botella, A. L. Garcia-Garcia, T. Wiegand, A. Giménez. 2020. Assessment of the key evolutionary traits that prevent extinctions in human-altered habitats using a spatially explicit in dividual-based model. Ecological Modelling 415: 108823
- Grimm, V., E. Revilla, U. Berger, F. Jeltsch, W. Mooij, S. F. Railsback, H. Thulke, J. Weiner, T. Wiegand, and D. L. DeAngelis. 2005 Pattern-oriented modeling of agent-based complex systems: lessons from ecology. Science 310:987-991.
- Hartig, F. J. Calabrese, B. Reineking, T. Wiegand, and A. Huth. 2011. Statistical inference for stochastic simulations models - theory and application. Ecology Letters 14:816-827
- Hartig, F., C. Dislich, T. Wiegand, and A. Huth. 2014. Approximate Bayesian parameterization of a complex tropical forest model. Biogeosciences 11: 1261–1272
- Jiménez-Franco, M.V., A. Giménez, R.C. Rodríguez-Caro, A. Sanz-Aguilar, F. Botella, J.D. Anadón, T. Wiegand, E. Graciá. 2020. Sperm storage reduces the strength of the mate-finding Allee effect. Ecology and Evolution 10:1938-194
- Jiménez-Franco, M.V., E. Graciá, R.C. Rodríguez-Caro, A. Sanz-Aguilar, J.D. Anadón, T. Wiegand, F. Botella, A. Giménez. 2022. Problems seeded in the past: lagged effects of historical land-use changes cause an extinction debt in long-lived species due to movement limitation. Landscape Ecology 37: 1331-1346
- Jiménez-Franco, M.V., E. Graciá, R.C. Rodríguez-Caro, J.D. Anadón, T. Wiegand, A. Giménez. 2024. Alternative vegetation trajectories through passive habitat rewilding: opposite effects for animal conservation. Landscape Ecology 39:78
- Kanagaraj, R., T. Wiegand, S. Kramer-Schadt, M. Anwar, and S.P. Goyal. 2011. Assessing habitat suitability for tiger in the fragmented Terai Arc Landscape of India and Nepal. Ecography 34: 970-981
- Kanagaraj, R. T. Wiegand, S. Kramer-Schadt, S.P. Goyal. 2013 Using individual-based movement models to assess inter-patch connectivity for large carnivores in fragmented landscapes. Biological Conservation 167: 298–309
- Kazmierczak, M., T. Wiegand, and A. Huth. 2014. A neutral vs. non-neutral parametrizations of a physiological forest gap model. Ecological Modelling 288: 94–102
- Kramer-Schadt, S., E Revilla, and T. Wiegand. 2005. Lynx reintroductions in fragmented landscapes of Germany: projects with future or misunderstood wildlife conservation? Biological Conservation 125: 169-182.
- Louzao, M. D. Pinaud, C. Peron, K. Delord, T. Wiegand, and H. Weimerskirch. 2011. Conserving pelagic habitats: seascape modelling of an oceanic top predator. Journal of Applied Ecology 48: 121–132.
- Louzao, M., T. Wiegand, F. Bartumeus and H. Weimerskirch. 2014. Coupling instantaneous energy-budget models and behavioural mode analysis to estimate optimal foraging strategy: an example with wandering albatrosses. Movement Ecology 2: 8
- Louzao, M; O. Aumont, T. Hothorn, T. Wiegand, and H. Weimerskirch. 2013. Foraging in a changing environment: habitat shifts of an oceanic predator over the last half century. Ecography 36: 57-67
- Martínez, I., T. Wiegand, J. J. Camarero, E. Batllori, and E. Gutiérrez. 2011. Elucidating demographic processes underlying tree line patterns: a novel approach to model selection for individual-based models using Bayesian methods and MCMC. American Naturalist 177: E136-E152
- Martínez, I., F. González Taboada, J. Naves, A. Fernández-Gil, and T. Wiegand. 2016. Decline and recovery of a large carnivore: environmental change and long-term trends in an endangered brown bear population. Proceedings R. Soc. B 283: 20161832
- May, F., A. Huth, and T. Wiegand. 2015. Moving beyond abundance distributions – neutral theory and spatial patterns in a tropical forest. Proceedings R. Soc. B 282: 20141657
- May, F., T. Wiegand, S. Lehmann, and A. Huth. 2016. Do abundance distributions and species aggregation correctly predict macroecological biodiversity patterns in tropical forests? Global Ecology and Biogeography 25: 575-585
- May, F., Wiegand, T., Huth, A., and J. Chase. 2020. Scale-dependent effects of conspecific negative density dependence and immigration on biodiversity maintenance. Oikos 129: 1072-1083
- Muñoz-Gallego, R., Wiegand, T., Traveset, A., and J. M. Fedriani. 2023a. From seed dispersal service to reproductive collapse: density-dependent outcome of a palm-mammal interaction. Oikos 10: e10002
- Muñoz-Gallego, R., Wiegand, T., Traveset, A., and J. M. Fedriani. 2023b. Sex-driven neighborhood effects on herbivory in the dioecious Mediterranean palm Chamaerops humilis L. Oecologia 203: 151-165.
- Perea, A.J., T. Wiegand, J. L. Garrido, P.J. Rey, and J.M. Alcántar. 2021. Legacy effects of seed dispersal and early recruitment shape spatially the species interactions networks in Mediterranean forests. Journal of Ecology 109: 3670 – 3684
- Perea, A.J., T. Wiegand, J. L. Garrido, P.J. Rey, and J.M. Alcántar. 2022. Spatial phylogenetic and phenotypic patterns reveal ontogenetic shifts in ecological processes of plant community assembly. Oikos 12: e09260
- Revilla, E., and T. Wiegand. 2008. Individual movement behavior, matrix heterogeneity and the dynamics of spatially structured populations. PNAS 105:19120-19125.
- Rhodes, J. R., T. Wiegand, C.A. McAlpine, H.P. Possingham, D. Lunney, J. Callaghan, and M. Bowen. 2006. Species Distribution Models and Conservation Planning in Semi-urban Landscapes. A Case Study for the Koala. Conservation Biology 20: 449-459.
- Rodríguez-Pérez, J., T. Wiegand, and A. Traveset. 2012a. Adult proximity and frugivore activity structure plant populations – spatial patterns after the disperser’s loss. Functional Ecology 26:1221–1229
- Rodríguez-Pérez, J., T. Wiegand, and L. Santamaria. 2012b. Frugivore behavior determines plant distribution: a spatially-explicit analysis of a plant-disperser interaction. Ecography 35: 113-123.
- Salazar Villegas, M. H., T. Wiegand, R. González Martínez, S. Rodríguez Buriticá, M. Qasim and E. Csaplovics. 2023. Spatial facilitation and competition regulate tree species assembly in a tropical dry forest. Frontiers in Forests and Global Change 6: 1028515.
- Schadt, S., E. Revilla, T. Wiegand, F. Knauer, P. Kaczensky, U. Breitenmoser, L. Bufka, J. Cerveny, P. Koubek, T. Huber, C. Stanisa, and L. Trepl 2002. Assessing the suitability of central European landscapes for the reintroduction of Eurasian lynx. Journal of Applied Ecology 39:189-203.
- Shen, G., T. Wiegand, X. Mi, and F. He. 2013. Quantifying spatial phylogenetic structures of fully mapped plant communities. Methods in Ecology and Evolution. 4: 1132-1141.
- Velázquez, E., I. Martínez, S. Getzin, K.A. Moloney, and T. Wiegand. 2016. An evaluation of the state of spatial point pattern analysis in ecology. Ecography 39: 1042–1055.
- Wang, X., T. Wiegand, N.J.B. Kraft, N.G. Swenson, S.J. Davies, Z. Hao, R. Howe, Y. Lin, K. Ma, X. Mi, S-H Su, I-F Sun, and A Wolf. 2016. Stochastic dilution effects weaken deterministic effects of niche-based processes on the spatial distribution of large trees in species rich forests. Ecology 97: 347-360
- Wiegand, T., and K. A. Moloney 2004. Rings, circles and null-models for point pattern analysis in ecology. Oikos 104: 209-229.
- Wiegand, T., S. J. Milton, C. Wissel. 1995. A simulation model for a shrub ecosystem in the semiarid Karoo, South Africa. Ecology 76:2205-2211.
- Wiegand, T., J. Naves, T. Stephan, A. Fernandez. 1998a. Assessing the risk of extinction for the brown bear (Ursus arctos) in the Cordillera Cantabrica, Spain. Ecological Monographs 68:539-571.
- Wiegand, T., K. Moloney, S. J. Milton. 1998b. Population dynamics, disturbance, and pattern evolution: identifying the fundamental scales of organization in a model ecosystem. American Naturalist 152:321-337.
- Wiegand, T., K. Moloney, J. Naves, F. Knauer. 1999. Finding the missing link between landscape structure and population dynamics: a spatially explicit perspective. American Naturalist 154:605-627.
- Wiegand, T., F. Jeltsch, I. Hanski, and V. Grimm. 2003. Using pattern-oriented modeling for revealing hidden information: a key for reconciling ecological theory and application. Oikos 100: 209-222.
- Wiegand, T., E. Revilla, and F. Knauer. 2004. Dealing with uncertainty in spatially explicit population models. Biodiversity and Conservation 13:53-78.
- Wiegand, T., J. J. Camarero, N. Rüger, and E. Gutiérrez. 2006a. Abrupt population changes in treeline ecotones along smooth gradients. Journal of Ecology 94: 880-892.
- Wiegand, T., Kissling, W.D., Cipriotti, P.A., and Aguiar, M.R. 2006. Extending point pattern analysis to objects of finite size and irregular shape. Journal of Ecology 94: 825-837.
- Wiegand, T., C.V.S. Gunatilleke, I.A.U.N. Gunatilleke, and A. Huth. 2007. How single species increase local diversity in tropical forests. PNAS 104:19029–19033.
- Wiegand, T., J. Naves and M. Garbulsky, and N. Fernández. 2008. Animal habitat quality and ecosystem functioning: exploring seasonal patterns using NDVI. Ecological Monographs 78: 87-103.
- Wiegand, T., A. Huth., and I. Martínez. 2009. Recruitment in tropical tree species: revealing complex spatial patterns. American Naturalist 174: E106 - E140
- Wiegand, T., and K.A. Moloney. 2014. A handbook of spatial point pattern analysis in ecology. Chapman and Hall/CRC press, Boca Raton, FL
- Wiegand, T., P. Grabarnik, and D. Stoyan. 2016. Envelope tests for spatial point patterns with and without simulation. Ecosphere 7(6):e01365
- Wiegand, T., F. May, M. Kazmierczak and A. Huth. 2017a. What drives the spatial distribution and dynamics of local species richness in tropical forest. Proceedings R. Soc. B 284: 20171503
- Wiegand, T., M. Uriarte, N.J.B. Kraft, G. Shen, X. Wang, and F. He. 2017b. Spatially explicit metrics of species diversity, functional diversity, and phylogenetic diversity: insights into plant community assembly processes. Annual Review of Ecology, Evolution, and Systematics 48:329–351
- Wiegand T., X. Wang, K.J. Anderson-Teixeira, N. Bourg, M. Cao, X. Ci, S.J. Davies, Z. Hao, R. Howe, W.J. Kress, J. Lian, J. Li, L. Lin, Y. Lin, K. Ma, W. McShea, X. Mi, S.-H. Su, I.-F. Sun, A. Wolf, W. Ye, and A. Huth. 2021. Consequences of spatial patterns for coexistence in species rich plant communities. Nature Ecology and Evolution 5: 965–973
